题目内容
8.(1+2x)(x-$\frac{1}{x}$)5的展开式中的常数项为-20.分析 求出原式的第二个因式中$\frac{1}{x}$项的系数,与第一个因式中2x的系数之积,即为所求的常数项.
解答 解:根据题意,得;
(1+2x)(x-$\frac{1}{x}$)5展开式中的常数项,
是(x-$\frac{1}{x}$)5的展开式中$\frac{1}{x}$项的系数与2x的系数之积;
(x-$\frac{1}{x}$)5的展开式的通项公式为:
Tr+1=${C}_{5}^{r}$•x5-r•${(-\frac{1}{x})}^{r}$=(-1)r•${C}_{5}^{r}$•x5-2r,
令5-2r=-1,解得r=3;
∴T3+1=-${C}_{5}^{3}$•$\frac{1}{x}$=-10•$\frac{1}{x}$,
∴展开式中的常数项为-10×2=-20.
故答案为:-20.
点评 本题考查了二项式系数性质的应用问题,熟练掌握二次项系数的性质是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
18.将函数f(x)=cos(x+$\frac{π}{6}$)图象上所有点的横坐标缩短为原来的$\frac{1}{2}$倍,纵坐标不变,得到函数g(x)图象,则函数g(x)的解析式为( )
| A. | g(x)=cos(2x+$\frac{π}{3}$) | B. | g(x)=cos(2x+$\frac{π}{6}$) | C. | g(x)=cos($\frac{x}{2}$+$\frac{π}{3}$) | D. | g(x)=cos($\frac{x}{2}$+$\frac{π}{6}$) |
17.某中学调查了某班全部50名同学参加数学兴趣小组和语文兴趣小组的情况,数据如表:(单位:人)
(1)从该班同学中随机选1名,求该同学至少参加上述一个兴趣小组的概率;
(2)在既参加数学兴趣小组,又参加语文兴趣小组的6个同学中,有4个男同学,2个女同学,现从这6个同学中随机抽取2人做进一步的调查,求抽取的2人中恰有1个女同学的概率.
| 参加数学兴趣小组 | 未参加数学兴趣小组 | |
| 参加语文兴趣小组 | 6 | 10 |
| 未参加语文兴趣小组 | 14 | 20 |
(2)在既参加数学兴趣小组,又参加语文兴趣小组的6个同学中,有4个男同学,2个女同学,现从这6个同学中随机抽取2人做进一步的调查,求抽取的2人中恰有1个女同学的概率.
18.已知a∈R,则a=1是复数$z=\frac{1+ai}{1-ai}$(i为虚数单位)为纯虚数的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
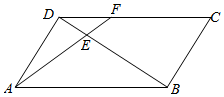 如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.
如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.