题目内容

实数x，y满足x2+2y2=6，则xy的最大值是
 
．
考点：基本不等式
专题：不等式的解法及应用
分析：利用基本不等式即可求出结果．
解答： 解：只考虑x•y＞0时即可．
∴6=x2+2y2≥2
2
xy，
化为xy≤
3
2
2
，当且仅当x=
2
y=±
6
2
时取等号．
xy的最大值是
3
2
2

故答案为：
3
2
2
．
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
相关题目
要使sinα-
3
cosα=4m-6对α∈R都有意义，求实数m的取值范围．
试判断函数f（x）=lg
1-x
1+x
在（-1，1）上的单调性．
下列双曲线中，与双曲线
x2
3
-y2=-1的离心率和渐近线都相同的是（　　）
A、
x2
3
-
y2
9
=1
B、
y2
3
-
x2
9
=1
C、
y2
3
-x2=1
D、
y2
3
-x2=-1
如图所示：矩形ABCD和矩形ABEF中，AF=AD，AM=DN，矩形ABEF可沿AB任意翻折．求证：当F、A、D不共线时，线段MN总平行于平面FAD．
函数y=ex+4e-x的最小值是
 
．
袋里装有7个球，每个球上分别标有从1到7的一个号码，这些球以等可能性（假定不受重量的影响）从袋里取出．已知号码n的球重
n2
3
-
7
3
n+8克，
（Ⅰ）如果任意取出一球，求其重量大于号码数的事件A的概率；
（Ⅱ）如果同时任意取出两球，求它们重量相同的事件B的概率．
定义在R上的函数f（x）满足：①对任意的x∈R，都有f（1+x）=f（1-x）成立；②对任意的x1，x2∈[1，+∞）且x1≠x2，都有
f(x1)-f(x2)
x1-x2
＜0成立，则（　　）
A、f（0）＜f（
2
）＜f（3）
B、f（3）＜f（
2
）＜f（0）
C、f（3）＜f（0）＜f（
2
）
D、f（0）＜f（3）＜f（
2
）
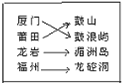福州、厦门、莆田、龙岩四个城市，它们分别有一个著名的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞，把福州、厦门、莆田、龙岩四个城市和它们的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞分别写成左右两列，现在一名旅游爱好者随机用4条线把左右全部连接起来，构成“一一对应”，已知连对的得2分，连错的得0分（如图所示是一种“一一对应”的连法，连对的只有一个“厦门→鼓浪屿”）．
（Ⅰ）求该旅游爱好者只得2分的概率；
（Ⅱ）该旅游爱好者的得分记为ξ，求ξ的分布列及数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网