题目内容
设数列{an}的首项a1为常数,且an+1=3n﹣2an(n∈N+).
(1)证明:{an﹣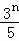 }是等比数列;
}是等比数列;
(2)若a1=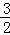 ,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
(3)若{an}是递增数列,求a1的取值范围.
解答: (1)证明:因为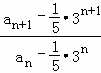 =
=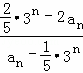 =﹣2,
=﹣2,
所以数列{an﹣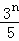 }是等比数列;
}是等比数列;
(2)解:{an﹣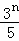 }是公比为﹣2,首项为a1﹣
}是公比为﹣2,首项为a1﹣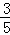 =
=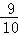 的等比数列.
的等比数列.
通项公式为an=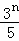 +(a1﹣
+(a1﹣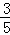 )(﹣2)n﹣1=
)(﹣2)n﹣1=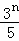 +
+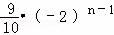
若{an}中存在连续三项成等差数列,则必有2an+1=an+an+2,
即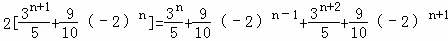
解得n=4,即a4,a5,a6成等差数列.
(3)解:如果an+1>an成立,
即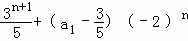 >
>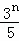 +(a1﹣
+(a1﹣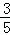 )(﹣2)n﹣1对任意自然数均成立.
)(﹣2)n﹣1对任意自然数均成立.
化简得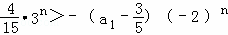 ,
,
当n为偶数时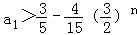 ,
,
因为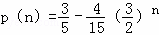 是递减数列,
是递减数列,
所以p(n)max=p(2)=0,即a1>0;
当n为奇数时,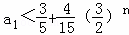 ,
,
因为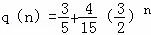 是递增数列,
是递增数列,
所以q(n)min=q(1)=1,即a1<1;
故a1的取值范围为(0,1).

练习册系列答案
相关题目
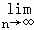
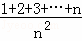 =
= 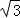 )处的切线方程为( )
)处的切线方程为( )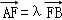 ,
,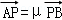 ,求证λ+μ为定值.
,求证λ+μ为定值.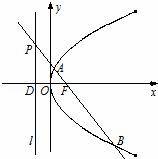
 有三个不相等的实根,则实
有三个不相等的实根,则实 数a的值是_____
数a的值是_____
 ,若
,若 且
且 ,
, 的值为___________
的值为___________ 的前
的前 项和为
项和为 ,则
,则 ___________
___________