题目内容
已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线C于A,B两点,若点P的纵坐标为m(m≠0),点D为准线l与x轴的交点.
(Ⅰ)求直线PF的方程;
(Ⅱ)求△DAB的面积S范围;
(Ⅲ)设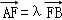 ,
,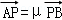 ,求证λ+μ为定值.
,求证λ+μ为定值.
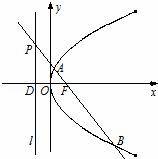
解:(Ⅰ)由题知点P,F的坐标分别为(﹣1,m),(1,0),
于是直线PF的斜率为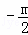 ,
,
所以直线PF的方程为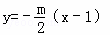 ,即为mx+2y﹣m=0.(3分)
,即为mx+2y﹣m=0.(3分)
(Ⅱ)设A,B两点的坐标分别为(x1,y1),(x2,y2),
由 得m2x2﹣(2m2+16)x+m2=0,
得m2x2﹣(2m2+16)x+m2=0,
所以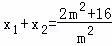 ,x1x2=1.
,x1x2=1.
于是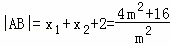 .
.
点D到直线mx+2y﹣m=0的距离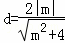 ,
,
所以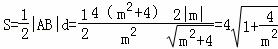 .
.
因为m∈R且m≠0,于是S>4,
所以△DAB的面积S范围是(4,+∞).(9分)
(Ⅲ)由(Ⅱ)及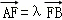 ,
,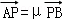 ,得(1﹣x1,﹣y1)=λ(x2﹣1,y2),(﹣1﹣x1,m﹣y1)
,得(1﹣x1,﹣y1)=λ(x2﹣1,y2),(﹣1﹣x1,m﹣y1)
=μ(x2+1,y2﹣m),
于是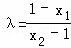 ,
,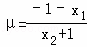 (x2≠±1).
(x2≠±1).
所以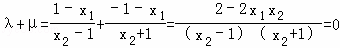 .
.
所以λ+μ为定值0.(14分)

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
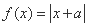 (
(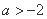 )的图象过点
)的图象过点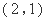 .
.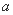 的值;
的值;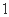 .试在该坐标系中作出函数
.试在该坐标系中作出函数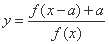 的简图,并写出(不需要证明)它的定义域、值域、奇偶性、单调区间.
的简图,并写出(不需要证明)它的定义域、值域、奇偶性、单调区间. 
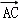 =(1,2),
=(1,2),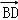 =(﹣4,2),则该四边形的面积为( )
=(﹣4,2),则该四边形的面积为( )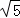 B.
B. 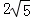 C. 5 D. 10
C. 5 D. 10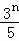 }是等比数列;
}是等比数列;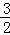 ,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由. 圈上的两点,它们的经度差为
圈上的两点,它们的经度差为 ,则A 、B两点间的球面距离为__
,则A 、B两点间的球面距离为__ 的最大值为1,则实数
的最大值为1,则实数

 ,若
,若 时恒成立,则实数的取值范围为____
时恒成立,则实数的取值范围为____