题目内容
圆x2+y2﹣4x=0在点P(1,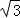 )处的切线方程为( )
)处的切线方程为( )
A. x+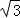 y﹣2=0 B. x+
y﹣2=0 B. x+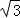 y﹣4=0 C. x﹣
y﹣4=0 C. x﹣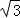 y+4=0 D. x﹣
y+4=0 D. x﹣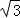 y+2=0
y+2=0
D
考点: 圆的切线方程.
专题: 计算题.
分析: 本题考查的知识点为圆的切线方程.(1)我们可设出直线的点斜式方程,联立直线和圆的方程,根据一元二次方程根与图象交点间的关系,得到对应的方程有且只有一个实根,即△=0,求出k值后,进而求出直线方程.(2)由于点在圆上,我们也可以切线的性质定理,即此时切线与过切点的半径垂直,进行求出切线的方程.
解答: 解:法一:
x2+y2﹣4x=0
y=kx﹣k+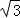 ⇒x2﹣4x+(kx﹣k+
⇒x2﹣4x+(kx﹣k+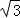 )2=0.
)2=0.
该二次方程应有两相等实根,即△=0,解得k=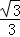 .
.
∴y﹣ =
=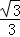 (x﹣1),
(x﹣1),
即x﹣ y+2=0.
y+2=0.
法二:
∵点(1, )在圆x2+y2﹣4x=0上,
)在圆x2+y2﹣4x=0上,
∴点P为切点,从而圆心与P的连线应与切线垂直.
又∵圆心为(2,0),∴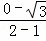 •k=﹣1.
•k=﹣1.
解得k=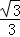 ,
,
∴切线方程为x﹣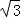 y+2=0.
y+2=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
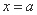 与函数
与函数 的图象至少有两个公共点;
的图象至少有两个公共点;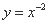 在
在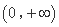 上是单调递减函数;
上是单调递减函数; (
(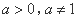 )的图象恒过定点
)的图象恒过定点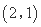 .
.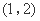 ,则函数
,则函数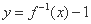
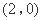 .
. ,则它的表面积为
,则它的表面积为  .
.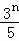 }是等比数列;
}是等比数列;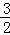 ,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由. f (a+1)与f (b+2)的大小关系是( )
f (a+1)与f (b+2)的大小关系是( ) 中,角
中,角 的对边分别为
的对边分别为 ,
, .
. 的值;
的值; ,且
,且 ,求c边的
,求c边的 长.
长.