题目内容
14.已知点A(-1,2),B(2,3),若直线l:kx-y-k+1=0与线段AB相交,则实数k的取值范围是( )| A. | (-∞,-$\frac{1}{2}$]∪[2,+∞) | B. | [{-$\frac{1}{2}$,2}] | C. | [-2,$\frac{1}{2}$] | D. | (-∞,-2]∪[$\frac{1}{2}$,+∞) |
分析 根据题意,分析可得A、B在直线的异侧或在直线上,进而可得[k×(-1)-2-k+1]×[2k-3-k+1]≤0,解可得k的取值范围,即可得答案.
解答 解:根据题意,若直线l:kx-y-k+1=0与线段AB相交,则A、B在直线的异侧或在直线上,
则有[k×(-1)-2-k+1]×[2k-3-k+1]≤0,
即(2k+1)(k-2)≥0,
解可得k≤-$\frac{1}{2}$或k≥2,即k的取值范围是(-∞,-$\frac{1}{2}$]∪[2,+∞);
故选:A.
点评 本题考查一元二次不等式表示平面区域,注意直线与线段AB相交,即A、B在直线的异侧或在直线上.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
5.某几何体的三视图如图所示,则其体积为( )
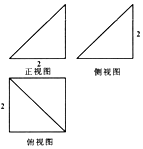

| A. | 4 | B. | 8 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
2.下列结论为真的个数是( )
(1)“x2+2x-3<0”是命题
(2)命题“若p,则q”的否命题是“若p,则¬q”
(3)当q是p的必要条件时,p是q的充分条件
(4)“若p不成立,则q不成立”等价于“若q成立,则p成立”
(1)“x2+2x-3<0”是命题
(2)命题“若p,则q”的否命题是“若p,则¬q”
(3)当q是p的必要条件时,p是q的充分条件
(4)“若p不成立,则q不成立”等价于“若q成立,则p成立”
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6. 如图是一个几何体在网格纸上的三视图,若面积最小网格均是边长为1的小正方形,则该几何体的体积为( )
如图是一个几何体在网格纸上的三视图,若面积最小网格均是边长为1的小正方形,则该几何体的体积为( )
 如图是一个几何体在网格纸上的三视图,若面积最小网格均是边长为1的小正方形,则该几何体的体积为( )
如图是一个几何体在网格纸上的三视图,若面积最小网格均是边长为1的小正方形,则该几何体的体积为( )| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
3.分析法证明命题中所说的“执果索因”是指寻求使命题成立的( )
| A. | 必要条件 | B. | 充分条件 | C. | 充要条件 | D. | 必要或充分条件 |