题目内容
19.7人站成两排队列,前排3人,后排4人.现将甲、乙、丙三人加入队列,前排加一人,后排加两人,其他人保持相对位置不变,则不同的加入方法种数为360.分析 分三步,第一步,从甲、乙、丙三人选一个加到前排,第二步,前排3人形成了4个空,任选一个空加一人,有4种,第三步,后排4分人,形成了5个空,任选一个空加一人,有5种,此时形成了6个空,任选一个空加一人,根据分步计数原理可得.
解答 解:第一步,从甲、乙、丙三人选一个加到前排,有3种,
第二步,前排3人形成了4个空,任选一个空加一人,有4种,
第三步,后排4分人,形成了5个空,任选一个空加一人,有5种,此时形成了6个空,任选一个空加一人,有6种,
根据分步计数原理可得3×4×5×6=360,
故答案为360.
点评 本题考查了分步计数原理,关键是分步,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
14.已知点A(-1,2),B(2,3),若直线l:kx-y-k+1=0与线段AB相交,则实数k的取值范围是( )
| A. | (-∞,-$\frac{1}{2}$]∪[2,+∞) | B. | [{-$\frac{1}{2}$,2}] | C. | [-2,$\frac{1}{2}$] | D. | (-∞,-2]∪[$\frac{1}{2}$,+∞) |
9.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的虚轴长为4,焦距为$4\sqrt{3}$,则双曲线的渐近线方程为( )
| A. | y=±$\sqrt{2}$x | B. | y=±2x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\frac{1}{2}$x |
 已知渡船在静水中速度$\overrightarrow{v_2}$的大小为$(\sqrt{6}+\sqrt{2})$m/s,河水流速$\overrightarrow{v_1}$的大小为2m/s.如图渡船船头方向与水流方向成$\frac{π}{4}$夹角,且河面垂直宽度为$600(\sqrt{3}+1)m$.
已知渡船在静水中速度$\overrightarrow{v_2}$的大小为$(\sqrt{6}+\sqrt{2})$m/s,河水流速$\overrightarrow{v_1}$的大小为2m/s.如图渡船船头方向与水流方向成$\frac{π}{4}$夹角,且河面垂直宽度为$600(\sqrt{3}+1)m$.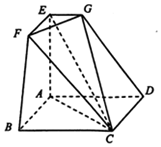 如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1,AE=3
如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1,AE=3