题目内容
3．设向量$\overrightarrow{a}$，$\overrightarrow{b}$不平行，向量$\overrightarrow{a}$+λ$\overrightarrow{b}$与3$\overrightarrow{a}$-$\overrightarrow{b}$平行，则实数λ=（ ）| A． | $\frac{1}{2}$ | B． | -$\frac{1}{3}$ | C． | -3 | D． | -2 |
分析 由向量平行可得存在实数μ使得$\overrightarrow{a}$+λ$\overrightarrow{b}$=μ（3$\overrightarrow{a}$-$\overrightarrow{b}$）=3μ$\overrightarrow{a}$-μ$\overrightarrow{b}$，对应系数相等可得λμ的方程组，解方程组可得．
解答 解：∵向量$\overrightarrow{a}$，$\overrightarrow{b}$不平行，向量$\overrightarrow{a}$+λ$\overrightarrow{b}$与3$\overrightarrow{a}$-$\overrightarrow{b}$平行，
∴存在实数μ使得$\overrightarrow{a}$+λ$\overrightarrow{b}$=μ（3$\overrightarrow{a}$-$\overrightarrow{b}$）=3μ$\overrightarrow{a}$-μ$\overrightarrow{b}$，
∴$\left\{\begin{array}{l}{1=3μ}\\{λ=-μ}\end{array}\right.$，解得$\left\{\begin{array}{l}{λ=-\frac{1}{3}}\\{μ=\frac{1}{3}}\end{array}\right.$
故选：B
点评 本题考查向量的平行线与共线，属基础题．
练习册系列答案
春雨教育同步作文系列答案
相关题目
11．
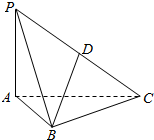如图，PA⊥平面ABC，PA=$\sqrt{2}$，AB=1，BC=$\sqrt{3}$，AC=2，D是PC的中点．
（1）求二面角B-PA-C的大小；
（2）求直线BD与平面ABC所成角的正切值．
如图，PA⊥平面ABC，PA=$\sqrt{2}$，AB=1，BC=$\sqrt{3}$，AC=2，D是PC的中点．（1）求二面角B-PA-C的大小；
（2）求直线BD与平面ABC所成角的正切值．
8．已知函数y=f（x）为奇函数且在R上的单调递增，若f（2m）+f（1-m）＞0，则实数m的取值范围是（ ）
| A． | （-1，2] | B． | （-1，+∞） | C． | （-1，4] | D． | [-1，+∞） |
《九章算术》中将底面的长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为蟞臑．在如图所示的阳马P-ABCD中，侧棱PD⊥底面ABCD，且PD=CD=BC，则当点E在下列四个位置：PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中，蟞臑有（ ）