题目内容
15. 《九章算术》中将底面的长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为蟞臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD=BC,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,蟞臑有( )
《九章算术》中将底面的长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为蟞臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD=BC,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,蟞臑有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分情况讨论:(1)当点E在PC中点时,证明BC⊥平面PCD,DE⊥平面PBC,可知四面体EBCD的四个面都是直角三角形,即可得出结论;
(2)当点E在PA中点时:以D为原点,分别以DA,DC,DP为x,y,z轴的正方向建立空间直角坐标系,设PD=DC=BC=1,则可求BC,BE,EC三边长不满足勾股定理,可得△EBC不是直角三角形,故故四面体E-BCD不是蟞臑.
(3)当点E在PB中点时:易证△BCE不是直角三角形(同上),可得四面体E-BCD不是蟞臑.
(4)当点E在PD中点时:由BC⊥平面ECD,DE⊥平面DBC,可知四面体EBCD的四个面都是直角三角形,即四面体EBCD是一个鳖臑.
解答 证明:(1)当点E在PC中点时: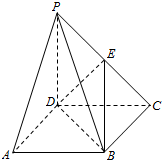
因为PD⊥底面ABCD,所以PD⊥BC,
因为ABCD为正方形,所以BC⊥CD,
因为PD∩CD=D,
所以BC⊥平面PCD,
因为DE?平面PCD,
所以BC⊥DE,
因为PD=CD,点E是PC的中点,
所以DE⊥PC,
因为PC∩BC=C,
所以DE⊥平面PBC,
由BC⊥平面PCD,DE⊥平面PBC,可知四面体EBCD的四个面都是直角三角形,
即四面体EBCD是一个鳖臑,其四个面的直角分别是∠BCD,∠BCE,∠DEC,∠DEB;
(2)当点E在PA中点时:如图,以D为原点,分别以DA,DC,DP为x,y,z轴的正方向建立空间直角坐标系,
设PD=DC=BC=1,则:C(0,1,0),B(1,1,0),D(0,0,0),E($\frac{1}{2}$,0,$\frac{1}{2}$),
可求:BC=1,BE=$\frac{\sqrt{6}}{2}$,EC=$\frac{\sqrt{6}}{2}$,三边长不满足勾股定理,可得△EBC不是直角三角形,
故故四面体E-BCD不是蟞臑.
(3)如下图当点E在PB中点时:易证△BCE不是直角三角形(同上),故四面体E-BCD不是蟞臑.
(4)如下图当点E在PD中点时:
由BC⊥平面ECD,DE⊥平面DBC,可知四面体EBCD的四个面都是直角三角形,
即四面体EBCD是一个鳖臑.
故选:B.
点评 本题考查线面垂直的判定与性质,考查学生分析解决问题的能力,属于中档题.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | -2 |
| A. | (-∞,-1] | B. | (2,+∞) | C. | (-1,2] | D. | [-1,2) |
| A. | {-1,1} | B. | {-1,3} | C. | {3,1,-1} | D. | {1,3} |
| A. | 若a∥α,b∥a⇒b∥α | B. | 若a∥α,b∥α,a?β,b?β⇒β∥α | ||
| C. | 若α∥β,b∥α⇒b∥β | D. | 若α∥β,a?α⇒a∥β |
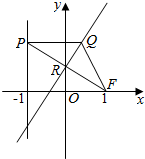 在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.