题目内容

18．以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，已知直线1的参数方程是$\left\{\begin{array}{l}{x=t+3}\\{y=\frac{\sqrt{3}}{3}t+\frac{3\sqrt{3}}{4}}\end{array}\right.$（t为参数），曲线C的极坐标方程是ρ=$\frac{6cosθ}{1-cos2θ}$，求直线l被曲线C截得的弦长．

分析 直线1的参数方程是$\left\{\begin{array}{l}{x=t+3}\\{y=\frac{\sqrt{3}}{3}t+\frac{3\sqrt{3}}{4}}\end{array}\right.$（t为参数），化为标准参数方程：$\left\{\begin{array}{l}{x=3+\frac{\sqrt{3}}{2}m}\\{y=\frac{3\sqrt{3}}{4}+\frac{1}{2}m}\end{array}\right.$，曲线C的极坐标方程是ρ=$\frac{6cosθ}{1-cos2θ}$，化为2ρ2sin2θ=6ρcosθ，利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$，即可化为直角坐标方程．把直线的参数方程代入抛物线方程，利用直线l被曲线C截得的弦长=|m1-m2|=$\sqrt{（{m}_{1}+{m}_{2}）^{2}-4{m}_{1}{m}_{2}}$，即可得出．

解答 解：直线1的参数方程是$\left\{\begin{array}{l}{x=t+3}\\{y=\frac{\sqrt{3}}{3}t+\frac{3\sqrt{3}}{4}}\end{array}\right.$（t为参数），化为标准参数方程：$\left\{\begin{array}{l}{x=3+\frac{\sqrt{3}}{2}m}\\{y=\frac{3\sqrt{3}}{4}+\frac{1}{2}m}\end{array}\right.$，
曲线C的极坐标方程是ρ=$\frac{6cosθ}{1-cos2θ}$，化为2ρ2sin2θ=6ρcosθ，化为直角坐标方程：y2=3x．
把直线的参数方程代入抛物线方程可得：$（\frac{3\sqrt{3}}{4}+\frac{1}{2}m）^{2}$=3$（3+\frac{\sqrt{3}}{2}m）$，
可得：4m2-12$\sqrt{3}$m-117=0，
∴m1+m2=3$\sqrt{3}$，m1m2=-$\frac{117}{4}$．
∴直线l被曲线C截得的弦长=|m1-m2|=$\sqrt{（{m}_{1}+{m}_{2}）^{2}-4{m}_{1}{m}_{2}}$=$\sqrt{（3\sqrt{3}）^{2}-4×（-\frac{117}{4}）}$=12．

点评 本题考查了极坐标化为直角坐标、弦长公式、直线参数方程的应用，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
8．函数y=$\sqrt{{{log}_{\frac{1}{2}}}（x-1）-1}$的定义域为（　　）
A．$（-∞，\frac{3}{2}]$B．$（1，\frac{3}{2}）$C．$（1，\frac{3}{2}]$D．$[\frac{3}{2}，+∞）$
9．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的离心率$e=\sqrt{2}$，F1、F2为其左右焦点，点P在C上，且$\overrightarrow{P{F_2}}•\overrightarrow{{F_1}{F_2}}=0$，$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=2$，O是坐标原点．
（1）求双曲线C的方程；
（2）过F2的直线l与双曲线C交于A，B两点，求$\overrightarrow{{F_1}A}•\overrightarrow{{F_1}B}$的取值范围．
6．已知函数$f（x）={cos^2}x+\sqrt{3}sinxcosx+a$的图象过点$（\frac{π}{6}，1）$．
（Ⅰ）求实数a的值及函数f（x）的最小正周期；
（Ⅱ）求函数f（x）在$[0，\frac{π}{2}]$上的最小值．
13．椭圆的两个焦点为F1（-1，0），F2（1，0），长轴的长为10，则椭圆的方程为$\frac{x^2}{25}+\frac{y^2}{24}=1$．
3．设向量$\overrightarrow{a}$，$\overrightarrow{b}$不平行，向量$\overrightarrow{a}$+λ$\overrightarrow{b}$与3$\overrightarrow{a}$-$\overrightarrow{b}$平行，则实数λ=（　　）
A．$\frac{1}{2}$B．-$\frac{1}{3}$C．-3D．-2
10．已知A={x|x2≥4}，B={x|x＞-2}，C={x|x2-3x+2≤0}．
（1）求A∩B及A∪C；
（2）若U=R，求（A∩C）∪（∁UB）
7．设集合A={x|8-2x＞0}，集合B={x|x=2n-1，n∈N*}，则A∩B等于（　　）
A．{-1，1}B．{-1，3}C．{3，1，-1}D．{1，3}
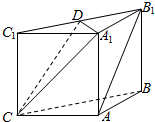8．如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，AB=AC=1，∠BAC=90°，点D是棱B1C1的中点．
（1）求证：A1D⊥平面BB1C1C；
（2）求证：AB1∥平面A1DC；
（3）求三棱锥C1-A1CD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网