题目内容
14.在极坐标系中,曲线C的方程为${ρ^2}=\frac{3}{{1+2{{cos}^2}θ}}$,点$R(2\sqrt{2},\frac{π}{4})$,以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(1)求曲线C的直角坐标方程及点R的直角坐标;
(2)设P为曲线C上一动点,以PR为对角线的矩形PQRS的一边垂直于极轴,求矩形PQRS周长的最小值及此时点P的直角坐标.
分析 (1)由极坐标转化为直角坐标即可;
(2)由参数方程,设出P的坐标,得到矩形的周长,根据三角函数的图象和性质即可求出最值.
解答  解:(1)由x=ρcosθ,y=ρsinθ,
解:(1)由x=ρcosθ,y=ρsinθ,
∴曲线C的直角坐标方程为$\frac{x^2}{1}+\frac{y^2}{3}=1$,点R的直角坐标为(2,2),
(2)曲线C的参数方程为$\left\{{\begin{array}{l}{x=cosα}\\{y=sinα}\end{array}}\right.(α$为参数,α∈[0,2π)),
设$P(cosα,\sqrt{3}sinα)$,如图,依题意可得:
|PQ|=2-cosα,$|{QR}|=2-\sqrt{3}sinα$,
∴矩形周长=$2|{PQ}|+2|{QR}|=4-2cosα+4-2\sqrt{3}sinα=8-4sin(α+\frac{π}{6})$,
∴当$α=\frac{π}{3}$时,周长的最小值为4,此时,点P的坐标为$(\frac{1}{2},\frac{3}{2})$.
点评 本题考查点的极坐标和直角坐标的互化,以及利用平面几何知识解决最值问题.利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
相关题目
2.函数f(x)=-x2-6x-1的减区间是( )
| A. | (-∞,+∞) | B. | (-3,+∞) | C. | (-∞,-3) | D. | (-3,3) |
5.已知复数z满足z(1+i)=1+ai(其中i是虚数单位,a∈R),则复数z在复平面内对应的点不可能位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.设向量$\overrightarrow{a}$,$\overrightarrow{b}$不平行,向量$\overrightarrow{a}$+λ$\overrightarrow{b}$与3$\overrightarrow{a}$-$\overrightarrow{b}$平行,则实数λ=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | -2 |
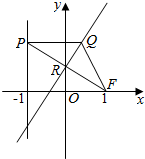 在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.