题目内容
8.已知函数y=f(x)为奇函数且在R上的单调递增,若f(2m)+f(1-m)>0,则实数m的取值范围是( )| A. | (-1,2] | B. | (-1,+∞) | C. | (-1,4] | D. | [-1,+∞) |
分析 根据函数奇偶性和单调性之间的关系,将不等式进行转化进行求解即可.
解答 解:∵f(x)是奇函数,
∴不等式f(2m)+f(1-m)>0等价为f(2m)>-f(1-m)=f(m-1),
∵y=f(x)在R上的单调递增,
∴2m>m-1,即m>-1,
故选:B
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系将不等式进行转化是解决本题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
18.已知集合M={x|x2-x-2<0},N={x|-1<x<1},则( )
| A. | M是N的真子集 | B. | N是M的真子集 | C. | M=N | D. | M∩N=φ |
3.设向量$\overrightarrow{a}$,$\overrightarrow{b}$不平行,向量$\overrightarrow{a}$+λ$\overrightarrow{b}$与3$\overrightarrow{a}$-$\overrightarrow{b}$平行,则实数λ=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | -2 |
13.在空间直角坐标系O-xyz中,向量$\overrightarrow{OA}$=(a,2,8),$\overrightarrow{OB}$=(2,7,0),若|AB|>7$\sqrt{2}$,则实数a的取值范围为( )
| A. | (-1,5) | B. | (-∞,-1) | C. | (5,+∞) | D. | (-∞,-1)∪(5,+∞) |
20.已知集合M={x|x+1≥0},N={x|-2<x<2},则M∩N=( )
| A. | (-∞,-1] | B. | (2,+∞) | C. | (-1,2] | D. | [-1,2) |
17.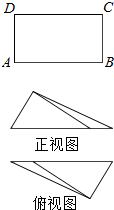 如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )
 如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
18.已知O为坐标原点,直线y=2与x2+y2+Dx-4y=0交于两点M,N,则∠MON=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |