题目内容
已知数列{an}满足a1=1,an+1=1-
,其中n∈N*
(1)设bn=
,求证:数列{bn}是等差数列;
(2)若cn=6n+(-1)n-1λ•2 bn是否存在λ,使得对任意n∈N+,都有cn+1>cn,若存在,求出λ的取值范围;若不存在,说明理由;
(3)证明::对一切正整数n,有
+
+…+
<
.
| 1 |
| 4an |
(1)设bn=
| 2 |
| 2an-1 |
(2)若cn=6n+(-1)n-1λ•2 bn是否存在λ,使得对任意n∈N+,都有cn+1>cn,若存在,求出λ的取值范围;若不存在,说明理由;
(3)证明::对一切正整数n,有
| 1 |
| b1(b1+1) |
| 1 |
| b2(b2+1) |
| 1 |
| bn(bn+1) |
| 13 |
| 42 |
考点:数列的求和,等差关系的确定,数列递推式
专题:综合题,分类讨论
分析:(1)利用等差数列的定义判断;(2)由cn+1>cn,得到λ的不等式,注意对n的奇偶性讨论,得到n的范围;(3)裂项求和即可.
解答:
解:(1)证明:bn+1-bn=bn=
-
=
-
=
-
=2
所以数列{bn}是等差数列,a1=1,b1=2,因此bn=2n.…(4分)
(2)cn=6n+(-1)n-1λ•2 bn=6n+(-1)n-1λ•4n,由cn+1>cn恒成立,则
6n+1+(-1)nλ•4n+1>6n+(-1)n-1λ•4n⇒6n+(-1)nλ•4n>0
当n为偶数时,λ>-
=-(
)n,∴λ>[-(
)n]max=-
当n为奇数时,λ<=
=(
)n,∴λ<[(
)n]min=
综上λ∈(-
,
)..…(9分)
(3)由(1)
=
=
<
=
=
-
(n≥2).
.
∴
+
+…+
<
+(
-
+
-
+…+
-
)=
-
<
.
| 2 |
| 2an+1-1 |
| 2 |
| 2an-1 |
| 2 | ||
2(1-
|
| 2 |
| 2an-1 |
| 4an |
| 2an-1 |
| 2 |
| 2an-1 |
所以数列{bn}是等差数列,a1=1,b1=2,因此bn=2n.…(4分)
(2)cn=6n+(-1)n-1λ•2 bn=6n+(-1)n-1λ•4n,由cn+1>cn恒成立,则
6n+1+(-1)nλ•4n+1>6n+(-1)n-1λ•4n⇒6n+(-1)nλ•4n>0
当n为偶数时,λ>-
| 6n |
| 4n |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
当n为奇数时,λ<=
| 6n |
| 4n |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
(3)由(1)
| 1 |
| bn(bn+1) |
| 1 |
| 2n(2n+1) |
| 4 |
| 16n2+8n |
| 4 |
| 16n2+8n-3 |
| 4 |
| (4n-1)(4n+3) |
| 1 |
| 4n-1 |
| 1 |
| 4n+3 |
.
∴
| 1 |
| b1(b1+1) |
| 1 |
| b2(b2+1) |
| 1 |
| bn(bn+1) |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 11 |
| 1 |
| 11 |
| 1 |
| 15 |
| 1 |
| 4n-1 |
| 1 |
| 4n+1 |
| 13 |
| 42 |
| 1 |
| 4n+3 |
| 13 |
| 42 |
点评:本题主要考查了等差数列的判断,数列的求和数列递推关系的综合应用,试题的综合性较强,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
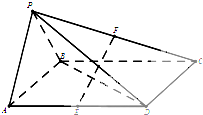 四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB=
四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB= 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=