题目内容
已知一个二次函数y=f(x)的抛物线先向左平移2个单位长度,再向下平移2个单位长度,此时抛物线过点(-1,-1),对称轴为x=-2,且在x轴上截得的线段长为2
,求f(x)的表达式.
| 2 |
考点:二次函数的性质,函数的图象与图象变化
专题:函数的性质及应用
分析:先求出平移后的函数的解析式,从而求出平移前的函数的解析式.
解答:
解:设平移后的解析式为:y=ax2+bx+c,
∴
,
解得:a=
,b=3,c=
,
∴y=
x2+3x+
=
(x+2)2-
,
∴二次函数y=f(x)的解析式为:
f(x)=
x2+
.
∴
|
解得:a=
| 3 |
| 4 |
| 5 |
| 4 |
∴y=
| 3 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
∴二次函数y=f(x)的解析式为:
f(x)=
| 3 |
| 4 |
| 1 |
| 4 |
点评:本题考查了二次函数的性质,求二次函数的解析式,考查函数的平移问题,是一道基础题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
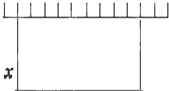 某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=
某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=