题目内容
15.在区间$[{-\frac{π}{4},\frac{2π}{3}}]$上任取一个数x,则函数$f(x)=3sin({2x-\frac{π}{6}})$的值不小于0的概率为( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{6}{11}$ | D. | $\frac{7}{12}$ |
分析 本题是几何概型的考查,利用区间长度的比即可求概率.
解答 解:∵函数$f(x)=3sin({2x-\frac{π}{6}})$,
当$x∈[{-\frac{π}{4},\frac{2π}{3}}]$时,$2x-\frac{π}{6}∈[{-\frac{2π}{3},\frac{7π}{6}}]$,
当$2x-\frac{π}{6}∈[{0,π}]$,即$x∈[{\frac{π}{12},\frac{7π}{12}}]$时,
f(x)≥0,
则所求概率为P=$\frac{{\frac{7π}{12}-\frac{π}{12}}}{{\frac{2π}{3}-({-\frac{π}{4}})}}=\frac{6}{11}$.
故选:C.
点评 本题考查了几何概型的概率求法;关键是正确选择测度比求概率.

练习册系列答案
相关题目
20.以下关于函数f(x)=sin2x-cos2x的命题,正确的是( )
| A. | 函数f(x)在区间$(0,\frac{2}{3}π)$上单调递增 | |
| B. | 直线$x=\frac{π}{8}$是函数y=f(x)图象的一条对称轴 | |
| C. | 点$(\frac{π}{4},0)$是函数y=f(x)图象的一个对称中心 | |
| D. | 将函数y=f(x)的图象向左平移$\frac{π}{8}$个单位,可得到$y=\sqrt{2}sin2x$的图象 |
7.已知函数$f(x)=\left\{{\begin{array}{l}{x+2}&{({x≤-1})}&{\;}\\{2x}&{({-1<x<2})}&{\;}\\{\frac{x^2}{2}}&{({x≥2})}&{\;}\end{array}}\right.$则$f[{f({-\frac{7}{4}})}]$=( )
| A. | $\frac{1}{4}$ | B. | -7 | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |
14.已知f(x)=sinx+cosx,则f($\frac{π}{12}$)的值为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
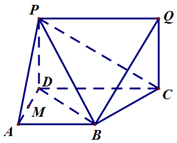 如图,在直角梯形ABCD中,AB⊥AD,AB∥CD,PD⊥面ABCD,QC⊥面ABCD,且AB=AD=PD=QC=$\frac{1}{2}$CD,
如图,在直角梯形ABCD中,AB⊥AD,AB∥CD,PD⊥面ABCD,QC⊥面ABCD,且AB=AD=PD=QC=$\frac{1}{2}$CD,