题目内容
14.已知f(x)=sinx+cosx,则f($\frac{π}{12}$)的值为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 将函数化简,再将x=$\frac{π}{12}$带入计算即可.
解答 解:f(x)=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)
则f($\frac{π}{12}$)=$\sqrt{2}$sin($\frac{π}{12}+\frac{3π}{12}$)=$\sqrt{2}$sin$\frac{π}{3}$=$\frac{\sqrt{6}}{2}$.
故选A.
点评 本题考查了辅助角公式的化简运用.比较基础.

练习册系列答案
相关题目
15.在区间$[{-\frac{π}{4},\frac{2π}{3}}]$上任取一个数x,则函数$f(x)=3sin({2x-\frac{π}{6}})$的值不小于0的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{6}{11}$ | D. | $\frac{7}{12}$ |
2.已知随机变量ε的分布列如下表:
求其数学期望、方差和标准差.
| ε | 0 | 1 | 2 | 3 | 4 |
| p | 0.2 | 0.4 | 0.3 | 0.08 | 0.02 |
3.在正四棱锥P-ABCD中,O为正方形ABCD的中心,$\overrightarrow{PE}$=λ$\overrightarrow{EO}$(2≤λ≤4),且平面ABE与直线PD交于F,$\overrightarrow{PF}$=f(λ)$\overrightarrow{PD}$,则( )
| A. | f(λ)=$\frac{λ}{λ+2}$ | B. | f(λ)=$\frac{2λ}{λ+6}$ | C. | f(λ)=$\frac{3λ}{λ+7}$ | D. | f(λ)=$\frac{4λ}{λ+9}$ |
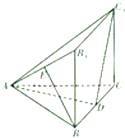 如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.
如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.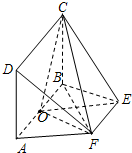 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.