题目内容
4.给出下列四个说法:①f(x)=x0与g(x)=1是同一个函数;
②y=f(x),x∈R与y=f(x+1),x∈R可能是同一个函数;
③y=f(x),x∈R与y=f(t),t∈R是同一个函数;
④定义域和值域相同的函数是同一个函数.
其中正确的个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 本题通过对函数的定义域、值域、解析式的研究,从而判断选项中的函数是否为同一函数,不是同一函数的,只要列举一个原因即可.
解答 解:命题①,f(x)=x0,x≠0,g(x)=1中,x∈R,故不是同一个函数;
命题②,若f(x)=1,则f(x+1)=1,y=f(x),故y=f(x+1)有可能是同一个函数,该选项正确;
命题③,y=f(x)与y=f(t)解析式相同,定义域一致,y=f(x)与y=f(t)是同一个函数;
命题④,函数y=x与y=x+1,定义域和值域均为R,但由于对应法则不同,故浊相同的函数,选项④不正确.
故选B.
点评 本题考查了函数的表示、函数的定义域、值域、解析式,本题难度不大,属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
15.在区间$[{-\frac{π}{4},\frac{2π}{3}}]$上任取一个数x,则函数$f(x)=3sin({2x-\frac{π}{6}})$的值不小于0的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{6}{11}$ | D. | $\frac{7}{12}$ |
12.一个几何体的三视图如图所示,则此几何体的表面积为( )
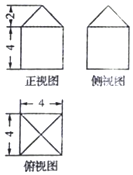

| A. | $80+16\sqrt{2}$ | B. | $96+13\sqrt{2}$ | C. | 96 | D. | 112 |
2.已知随机变量ε的分布列如下表:
求其数学期望、方差和标准差.
| ε | 0 | 1 | 2 | 3 | 4 |
| p | 0.2 | 0.4 | 0.3 | 0.08 | 0.02 |
3.在正四棱锥P-ABCD中,O为正方形ABCD的中心,$\overrightarrow{PE}$=λ$\overrightarrow{EO}$(2≤λ≤4),且平面ABE与直线PD交于F,$\overrightarrow{PF}$=f(λ)$\overrightarrow{PD}$,则( )
| A. | f(λ)=$\frac{λ}{λ+2}$ | B. | f(λ)=$\frac{2λ}{λ+6}$ | C. | f(λ)=$\frac{3λ}{λ+7}$ | D. | f(λ)=$\frac{4λ}{λ+9}$ |
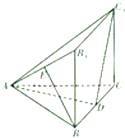 如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.
如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.