题目内容
1．
如图，利用随机模拟的方法可以估计图中由曲线y=$\frac{{x}^{2}}{2}$与两直线x=2及y=0所围成的阴影部分的面积S
①利用计算机先产生N组均匀随机数（xi，yi）（i=1，2，3，…N），xi∈[0，2]，yi∈[0，2]
②生成N个点（xi，yi），并统计满足条件yi＜$\frac{{{x}_{i}}^{2}}{2}$的点的个数N1，已知某同学用计算机做模拟试验结果，当N=1000时，N1=332，则据此可估计S的值为1.328．
分析 先由计算器做模拟试验结果试验估计，满足条件y＜$\frac{{x}^{2}}{2}$的点（x，y）的概率，再转化为几何概型的面积类型求解．
解答 解：根据题意：满足条件y＜$\frac{{x}^{2}}{2}$的点（x，y）的概率是 $\frac{332}{1000}$，
矩形的面积为10，设阴影部分的面积为s，
则有 $\frac{S}{4}$=率是 $\frac{332}{1000}$，
∴S=1.328，
故答案为：1.328．
点评 本题主要考查模拟方法估计概率以及几何概型中面积类型，将两者建立关系，引入方程思想．
练习册系列答案
相关题目
11．在区间[0，1]上随机取两个数x和y，则$y≥|{x-\frac{1}{2}}|$的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{4}$ |
12．已知Sn是数列{an}的前n项之和，a1=2，2Sn+1=Sn+4（n∈N*），则函数f（n）=Sn的值域是（ ）
| A． | （0，2] | B． | [2，4） | C． | [2，+∞） | D． | [2，3] |
9．sin40°sin10°+cos40°sin80°=（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | cos50° | D． | $\frac{{\sqrt{3}}}{2}$ |
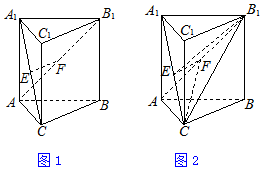如图，三棱柱ABC-A1B1C1中，侧棱AA1与底面垂直，∠ACB=90°，AC=BC，AA1=AB=2，E，F分别是A1C，AB1的中点．