题目内容
6.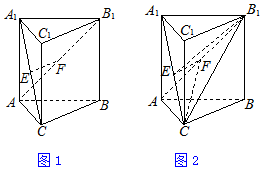 如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.(Ⅰ)证明:EF∥平面ABC
(Ⅱ)求三棱锥E-B1FC的体积.
分析 (Ⅰ)连结A1B,与AB1的交点即为F,推导出EF∥BC,由此能证明EF∥平面ABC.
(Ⅱ)三棱锥E-B1FC的体积${V}_{E-{B}_{1}FC}$=$\frac{1}{2}$${V}_{E-{B}_{1}AC}$=$\frac{1}{2}{V}_{{B}_{1}-AEC}$,由此能求出三棱锥E-B1FC体积.
解答 (本小题满分12分)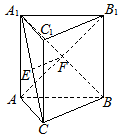
证明:(Ⅰ)连结A1B,与AB1的交点即为F,
∵E、F分别是A1C、A1B的中点,
∴EF∥BC,
又EF?平面ABC,BC?平面ABC,
∴EF∥平面ABC.
解:(Ⅱ)∵三棱锥E-B1FC的体积:
${V}_{E-{B}_{1}FC}$=$\frac{1}{2}$${V}_{E-{B}_{1}AC}$=$\frac{1}{2}{V}_{{B}_{1}-AEC}$,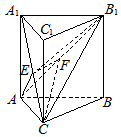
∵∠ACB=90°,AA1=AB=2,
∴$AC=BC=\sqrt{2}$,
又BC⊥AC,BC⊥CE,∴BC⊥平面AEC,
∴${V}_{E-{B}_{1}FC}$=$\frac{1}{2}×\frac{1}{3}(\frac{1}{2}×\sqrt{2}×1)×\sqrt{2}$=$\frac{1}{6}$,
∴三棱锥E-B1FC体积为$\frac{1}{6}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
16.三棱锥P-ABC中,底面△ABC满足BA=BC,$∠ABC=\frac{π}{2}$,P在面ABC的射影为AC的中点,且该三棱锥的体积为$\frac{9}{2}$,当其外接球的表面积最小时,P到面ABC的距离为( )
| A. | 2 | B. | 3 | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
14.定义一个对应法则f:P(m,n)→P'($\sqrt{m}$,$\sqrt{n$)(m≥0,n≥0),比如P(2,4)→P'($\sqrt{2}$,2),已知点A(2,6)和点B(6,2),M是线段AB上的动点,点M在法则f下的对应点为M',当M在线段AB上运动时,点M'的轨迹为( )
| A. | 线段 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 抛物线的一部分 |
18.已知三棱锥S-ABC外接球的直径SC=6,且AB=BC=CA=3,则三棱锥S-ABC的体积为( )
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{{9\sqrt{2}}}{4}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{9\sqrt{2}}}{2}$ |
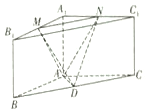 如下图所示的三棱柱ABC-A1B1C1中,棱AA1⊥底面A1B1C1,AB=AC=AA1,∠ABC=30°,M,N,D分别是A1B1,A1C1,BC的中点.
如下图所示的三棱柱ABC-A1B1C1中,棱AA1⊥底面A1B1C1,AB=AC=AA1,∠ABC=30°,M,N,D分别是A1B1,A1C1,BC的中点. 如图,利用随机模拟的方法可以估计图中由曲线y=$\frac{{x}^{2}}{2}$与两直线x=2及y=0所围成的阴
如图,利用随机模拟的方法可以估计图中由曲线y=$\frac{{x}^{2}}{2}$与两直线x=2及y=0所围成的阴 已知圆O:x2+y2=r2,直线$x+2\sqrt{2}y+2=0$与圆O相切,且直线l:y=kx+m与椭圆C:$\frac{x^2}{2}+{y^2}=1$相交于P、Q两点,O为原点.
已知圆O:x2+y2=r2,直线$x+2\sqrt{2}y+2=0$与圆O相切,且直线l:y=kx+m与椭圆C:$\frac{x^2}{2}+{y^2}=1$相交于P、Q两点,O为原点.