题目内容
12.已知Sn是数列{an}的前n项之和,a1=2,2Sn+1=Sn+4(n∈N*),则函数f(n)=Sn的值域是( )| A. | (0,2] | B. | [2,4) | C. | [2,+∞) | D. | [2,3] |
分析 求出数列的首项,利用an=Sn-Sn-1,推出数列的关系式,判断数列是等比数列,求出数列的和,然后求解值域.
解答 解:由2Sn+1=Sn+4,a1=2⇒a2=1,
2Sn=Sn-1+4(n≥2)⇒2an+1=an(n≥2),
n=1时,上式成立⇒{an}是首项为2,公比为$\frac{1}{2}$的等比数列,
$f(n)={S_n}=4({1-\frac{1}{2^n}})∈[2,\;\;4)$,
故选:B.
点评 本题考查数列的递推关系式的应用,等比数列的判断,数列的函数特征的应用,考查计算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.已知集合A={x|x>0},函数$f(x)=\sqrt{(2-x)(x-3)}$的定义域为集合B,则A∩B=( )
| A. | [3,+∞) | B. | [2,3] | C. | (0,2]∪[3,+∞) | D. | (0,2] |
4.点P(x,y)的坐标满足约束条件$\left\{\begin{array}{l}x-2y≥0\\ x+2y+4≥0\\ 7x+2y-8≤0\end{array}\right.$,由点P向圆C:(x+2)2+(y-1)2=1作切线PA,切点为A,则线段|PA|的最小值为( )
| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{55}}}{5}$ | C. | $\sqrt{19}$ | D. | $\frac{{\sqrt{33}}}{2}$ |
 如图所示的几何体ABCDE,EA⊥平面ABC,EA∥DC,AB⊥AC,EA=AB=AC=2DC,M是线段BD上的动点.
如图所示的几何体ABCDE,EA⊥平面ABC,EA∥DC,AB⊥AC,EA=AB=AC=2DC,M是线段BD上的动点.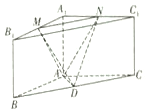 如下图所示的三棱柱ABC-A1B1C1中,棱AA1⊥底面A1B1C1,AB=AC=AA1,∠ABC=30°,M,N,D分别是A1B1,A1C1,BC的中点.
如下图所示的三棱柱ABC-A1B1C1中,棱AA1⊥底面A1B1C1,AB=AC=AA1,∠ABC=30°,M,N,D分别是A1B1,A1C1,BC的中点. 如图,利用随机模拟的方法可以估计图中由曲线y=$\frac{{x}^{2}}{2}$与两直线x=2及y=0所围成的阴
如图,利用随机模拟的方法可以估计图中由曲线y=$\frac{{x}^{2}}{2}$与两直线x=2及y=0所围成的阴