题目内容
已知向量
=(cosθ,sinθ),
=(1,-2),若
∥
,则代数式
的值是( )
| a |
| b |
| a |
| b |
| 2sinθ-cosθ |
| sinθ+cosθ |
A、
| ||
B、
| ||
| C、5 | ||
D、
|
考点:三角函数的化简求值,平面向量共线(平行)的坐标表示,同角三角函数间的基本关系
专题:三角函数的求值
分析:利用共线向量的关系,求出正弦函数与余弦函数的关系,代入所求表达式求解即可.
解答:
解:向量
=(cosθ,sinθ),
=(1,-2),若
∥
,
可得:sinθ=-2cosθ.
=
=5.
故选:C.
| a |
| b |
| a |
| b |
可得:sinθ=-2cosθ.
| 2sinθ-cosθ |
| sinθ+cosθ |
| -4cosθ-cosθ |
| -2cosθ+cosθ |
故选:C.
点评:本题考查三角函数的化简求值,向量共线定理的应用,考查计算能力.

练习册系列答案
相关题目
计算:[(-
)2]-1=( )
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
若m,n是正整数,则m+n>mn成立的充要条件是( )
| A、m,n都等于1 |
| B、m,n都不等于2 |
| C、m,n都大于1 |
| D、m,n至少有一个等于1 |
若y=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的最小值为-2,其图象相邻最高点与最低点横坐标之差为2π,且图象过点(0,1),则其解析式是( )
| π |
| 2 |
A、y=2sin(x+
| ||||
B、y=2sin(x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(
|
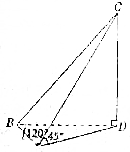 如图,A,B是海平面上的两个点,相距800m,在A点测得山顶C的仰角为45°,∠BAD=120°,又在B点测得∠ABD=45°,其中D是点C到水平面的射线,则山高CD=
如图,A,B是海平面上的两个点,相距800m,在A点测得山顶C的仰角为45°,∠BAD=120°,又在B点测得∠ABD=45°,其中D是点C到水平面的射线,则山高CD=