题目内容
已知直角△ABC的斜边AB=2
，O为斜边AB的中点，若P为线段OC上的动点，则（
+
）•
的最大值是 ．
| 2 |
| PA |
| PB |
| CP |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由中点向量的表示形式得，
+
=2
，再运用共线向量的数量积形式得，（
+
）•
=2
•
=2|
|•|
|，再运用二次函数，即可求出最大值．
| PA |
| PB |
| PO |
| PA |
| PB |
| CP |
| PO |
| CP |
| PO |
| CP |
解答：
解：∵O为斜边AB的中点，
∴
+
=2
∴（
+
）•
=2
•
=2|
|•|
|
∵P为线段OC上的动点，|
|+|
|=
，
∴2|
|•|
|=2|
|•（
-|
|）
=-2|
|2+2
|
|
=-2（|
|-
）2+1，
故当|
|=
时，取最大值为1．
故答案为：1．
∴
| PA |
| PB |
| PO |
∴（
| PA |
| PB |
| CP |
| PO |
| CP |
| PO |
| CP |
∵P为线段OC上的动点，|
| PO |
| CP |
| 2 |
∴2|
| PO |
| CP |
| PO |
| 2 |
| PO |
=-2|
| PO |
| 2 |
| PO |
=-2（|
| PO |
| ||
| 2 |
故当|
| PO |
| ||
| 2 |
故答案为：1．
点评：本题考查平面向量的数量积的定义，中点向量的表示形式，以及应用二次函数求最值，是一道中档题．
练习册系列答案
名校课堂系列答案
相关题目
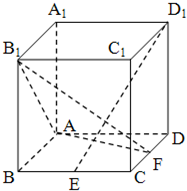如图，在正方体ABCD-A1B1C1D1中，点E是棱BC的中点，点F是棱CD上的动点．当