题目内容
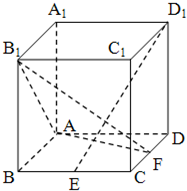如图，在正方体ABCD-A1B1C1D1中，点E是棱BC的中点，点F是棱CD上的动点．当| CF |
| FD |
考点：直线与平面垂直的性质
专题：证明题,空间位置关系与距离
分析：要D1E⊥平面AB1F，先确定D1E⊥平面AB1F内的两条相交直线，由三垂线定理易证D1E⊥AB1，同理证明D1E⊥AF即可．
解答：
解：连接A1B，则A1B是D1E在面ABB1A内的射影
∵AB1⊥A1B，∴D1E⊥AB1，
于是D1E⊥平面AB1F?D1E⊥AF．
连接DE，则DE是D1E在底面ABCD内的射影．
∴D1E⊥AF?DE⊥AF．
∵ABCD是正方形，E是BC的中点．
∴当且仅当F是CD的中点时，DE⊥AF，
即当点F是CD的中点时，D1E⊥平面AB1F．
∴
=1时，D1E⊥平面AB1F．
∵AB1⊥A1B，∴D1E⊥AB1，
于是D1E⊥平面AB1F?D1E⊥AF．
连接DE，则DE是D1E在底面ABCD内的射影．
∴D1E⊥AF?DE⊥AF．
∵ABCD是正方形，E是BC的中点．
∴当且仅当F是CD的中点时，DE⊥AF，
即当点F是CD的中点时，D1E⊥平面AB1F．
∴
| CF |
| FD |
点评：本小题主要考查线面关系和正方体等基础知识，考查空间想象能力和推理运算能力．
练习册系列答案
相关题目
如图，已知四棱锥P-ABCD的底面为菱形，PA⊥面ABCD，且PA=AB，∠BAD=60°，E、F分别是PA、BC的中点．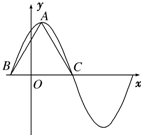
函数f（x）=3cos2