题目内容
7.已知函数f(x)=Asin(2x+$\frac{π}{3}$),(A>0)的最大值是2.(1)求A的值;
(2)在给定的坐标系中取合适长度作出f(x)在[0,π]的图象;
(3)在(2)的图象中,若直线y=m(-2<m<2,且m≠$\sqrt{3}$)与y=f(x),x∈[0,π]的图象有两个不同交点x1,x2,试求x1+x2的值.
分析 (1)根据三角函数的最值性质进行求解即可;
(2)根据五点作图法,即可在给定的平面直角坐标系中作出该函数在x∈[0,π]的图象;
(3)当x∈[0,π]时,根据实数m的不同取值,结合函数f(x)的图象结合三角函数的对称性进行求解即可.
解答 解:(1)∵f(x)=Asin(2x+$\frac{π}{3}$),(A>0)的最大值是2,
∴A=2.
(2)列表
| x | 0 | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | π |
| $2x+\frac{π}{3}$ | $\frac{π}{3}$ | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π | $\frac{7π}{3}$ |
| f(x) | $\sqrt{3}$ | 2 | 0 | -2 | 0 | $\sqrt{3}$ |
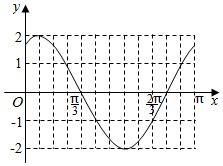
(3)
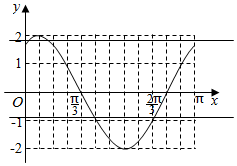 若-2<m<$\sqrt{3}$,则y=m与y=f(x),x∈[0,π]的图象有两个不同交点x1,x2,关于$\frac{7π}{12}$对称,
若-2<m<$\sqrt{3}$,则y=m与y=f(x),x∈[0,π]的图象有两个不同交点x1,x2,关于$\frac{7π}{12}$对称,则x1+x2=2×$\frac{7π}{12}$=$\frac{7π}{6}$,
若$\sqrt{3}$<m<2,y=m与y=f(x),x∈[0,π]的图象有两个不同交点x1,x2,关于$\frac{π}{12}$对称,
则x1+x2=2×$\frac{π}{12}$=$\frac{π}{6}$,
综上x1+x2的值为$\frac{π}{6}$或$\frac{7π}{6}$.
点评 本题主要考查三角函数的图象和性质,要求熟练掌握五点法作图.

练习册系列答案
相关题目
6.等差数列{an}中,a3=5,S6=36,则S9=( )
| A. | 17 | B. | 19 | C. | 81 | D. | 100 |
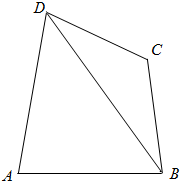 如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求
如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求