题目内容
13.设复数z满足(1+i)z=2,则z的共轭复数$\overline{z}$=( )| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
分析 利用复数的除法化简求解复数,即可得到共轭复数.
解答 解:复数z满足(1+i)z=2,
可得z=$\frac{2}{1+i}$=$\frac{2(1-i)}{(1+i)(1-i)}$=1-i.
则z的共轭复数$\overline{z}$=1+i.
故选:D.
点评 本题考查复数的基本运算,复数的基本概念的应用,是基础题.

练习册系列答案
相关题目
3.已知函数f(x)和g(x)是两个定义在区间M上的函数,若对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0),则称f(x)与g(x)在区间M上是“相似函数”.若f(x)=ax2+2(a-1)x-2lnx+b(a,b∈R)与g(x)=x+$\frac{1}{x}$在区间[$\frac{1}{2}$,2]上是“相似函数”,则a,b的值分别是( )
| A. | a=1,b=1 | B. | a=-1,b=-1 | C. | a=1,b=-1 | D. | a=-1,b=1 |
1.公比不为1的等比数列{an}满足a5a6+a4a7=18,若a1am=9,则m的值为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
3.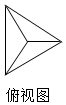 一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )
一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )
 一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )
一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\sqrt{3}$ |
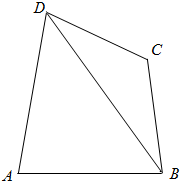 如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求
如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求