题目内容
14.已知f(x)=ex(sinx-cosx),则函数f(x)的图象x=$\frac{π}{2}$处的切线的斜率为2e${\;}^{\frac{π}{2}}$.分析 求得函数的导数,由导数的几何意义,代入x=$\frac{π}{2}$,即可得到所求切线的斜率.
解答 解:f(x)=ex(sinx-cosx)的导数为
f′(x)=2sinx•ex,
可得图象在x=$\frac{π}{2}$处的切线的斜率为
2sin$\frac{π}{2}$•e${\;}^{\frac{π}{2}}$=2e${\;}^{\frac{π}{2}}$.
故答案为:2e${\;}^{\frac{π}{2}}$.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,正确求导是解题的关键,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
4.已知数列{an}满足a1=1,an+1•an=2n(n∈N*),则S2016=( )
| A. | 22016-1 | B. | 3•21008-3 | C. | 3•21008-1 | D. | 3•21007-2 |
2.已知α为锐角,且$tanα=\sqrt{2}-1$,函数$f(x)={x^2}tan2α+x•sin(2α+\frac{π}{4})$,数列{an}的首项${a_1}=\frac{1}{2}\;,\;{a_{n+1}}=f({a_n})$,则有( )
| A. | an+1>an | B. | an+1≥an | C. | an+1<an | D. | an+1≤an |
9.设i为虚数单位,则复数$\frac{1-i}{i}$的共轭复数所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知i为虚数单位,若复数z满足|z-3-4i|=1,则|z|的最大值为( )
| A. | 4 | B. | 5 | C. | 4$\sqrt{2}$ | D. | 6 |
 如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险.
如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险. 在如图所示的直角三角形ABP中,已知直角边AB=2,BP=4,C、D分别为BP、AP的中点,将三角形DCP沿CD折起,使得面PBC⊥面ABCD,且PB=2,连接PB,PA得到四棱锥P-ABCD.
在如图所示的直角三角形ABP中,已知直角边AB=2,BP=4,C、D分别为BP、AP的中点,将三角形DCP沿CD折起,使得面PBC⊥面ABCD,且PB=2,连接PB,PA得到四棱锥P-ABCD.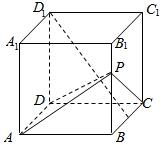 在边长为a的正方体ABCD-A1B1C1D1中,点P从B点开始按路径B→B1→C1→C运动,设从B点列P点的路程为x,V(x)表示空间几何体的体积,其中四校锥P-ABCD的体积为V1(x),剩余空间几何体的体积为V2(x).则f(x)=$\frac{{V}_{1}(x)}{{V}_{2}(x)}$的图象为( )
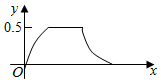
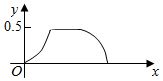
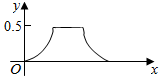
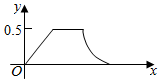
在边长为a的正方体ABCD-A1B1C1D1中,点P从B点开始按路径B→B1→C1→C运动,设从B点列P点的路程为x,V(x)表示空间几何体的体积,其中四校锥P-ABCD的体积为V1(x),剩余空间几何体的体积为V2(x).则f(x)=$\frac{{V}_{1}(x)}{{V}_{2}(x)}$的图象为( )