题目内容
19. 在如图所示的直角三角形ABP中,已知直角边AB=2,BP=4,C、D分别为BP、AP的中点,将三角形DCP沿CD折起,使得面PBC⊥面ABCD,且PB=2,连接PB,PA得到四棱锥P-ABCD.
在如图所示的直角三角形ABP中,已知直角边AB=2,BP=4,C、D分别为BP、AP的中点,将三角形DCP沿CD折起,使得面PBC⊥面ABCD,且PB=2,连接PB,PA得到四棱锥P-ABCD.(1)求证:PA⊥BD;
(2)求二面角P-BD-C的正切值.
分析 (1)建立空间坐标系,气促PA,BD的向量坐标,利用向量法进行证明.
(2)利用向量法求出平面的法向量,利用向量法进行求解即可求二面角的正切值.
解答 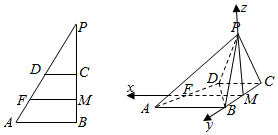 (1)证明:∵PB=PC=BC=2,∴△PBC是正三角形,
(1)证明:∵PB=PC=BC=2,∴△PBC是正三角形,
取CB的中点M,则PM⊥BC,
∵面PBC⊥面ABCD,∴PM⊥面ABCD,
建立以M为坐标原点,MF,MB,MP分别为x,y,z轴的空间直角坐标系如图:
∵AB=2,BP=4,C、D分别为BP、AP的中点,
∴A(2,1,0),B(0,1,0),D(1,-1,0),P(0,0,$\sqrt{3}$),
则$\overrightarrow{PA}$=(2,1,-$\sqrt{3}$),$\overrightarrow{BD}$=(1,-2,0),
则$\overrightarrow{PA}$•$\overrightarrow{BD}$=(2,1,-$\sqrt{3}$)•(1,-2,0)=2-2=0,
则$\overrightarrow{PA}$⊥$\overrightarrow{BD}$,即PA⊥BD.
(2)平面BDC的法向量为$\overrightarrow{m}$=(0,0,1),
设平面PBD的法向量为$\overrightarrow{n}$=(x,y,z),
$\overrightarrow{BD}$=(1,-2,0),$\overrightarrow{BP}$=(0,-1,$\sqrt{3}$),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BD}=0}\\{\overrightarrow{n}•\overrightarrow{BP}=0}\end{array}\right.$,则$\left\{\begin{array}{l}{x-2y=0}\\{-y+\sqrt{3}z=0}\end{array}\right.$,
令z=1,则y=$\sqrt{3}$,x=2$\sqrt{3}$,
即$\overrightarrow{n}$=(2$\sqrt{3}$,$\sqrt{3}$,1),
$cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}$=$\frac{1}{\sqrt{12+3+1}}=\frac{1}{\sqrt{16}}$=$\frac{1}{4}$,
则sin<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\sqrt{1-(\frac{1}{4})^{2}}$=$\sqrt{\frac{15}{16}}$=$\frac{\sqrt{15}}{4}$,
在tan<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\frac{\sqrt{15}}{4}}{\frac{1}{4}}$=$\sqrt{15}$.
点评 本题主要考查直线垂直的判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案| A. | A∩B=B | B. | A∪B=A | C. | A?B | D. | ∁RA=B |
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A. | 8.3 | B. | 8.2 | C. | 8.1 | D. | 8 |
 如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )
如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )| A. | “合情推理”的下位 | B. | “演绎推理”的下位 | ||
| C. | “直接证明”的下位 | D. | “间接证明”的下位 |
| A. | $\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
| A. | k≥0 | B. | k>1 | C. | k>0 | D. | k<0 |
| A. | 是奇函数,且在(0,+∞)上是增函数 | B. | 是奇函数,且在(0,+∞)上是减函数 | ||
| C. | 是偶函数,且在(0,+∞)上是减函数 | D. | 是偶函数,且在(0,+∞)上是增函数 |