题目内容
5. 如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险.
如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险.(1)mcosαcosβ>nsin(α-β)
(2)mcosαcosβ<nsin(α-β)
(3)$\frac{m}{n}>tanα-tanβ$
(4)$\frac{m}{tanα•tanβ}<\frac{n}{tanα-tanβ}$.
分析 先确定∠MAB、∠AMB的值,再作MC⊥AB,根据正弦定理可求得BM的关系式,然后根据x=BM•cosβ求出CM的值,只要x>n就没有触礁危险,从而得到答案.
解答 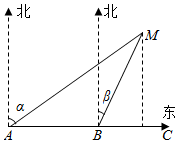 解:由题意可知,∠MAB=$\frac{π}{2}$-α,∠AMB=α-β
解:由题意可知,∠MAB=$\frac{π}{2}$-α,∠AMB=α-β
过M作MC⊥AB于C,设CM=x,
根据正弦定理可得$\frac{m}{sin(α-β)}=\frac{BM}{sin(\frac{π}{2}-α)}=\frac{BM}{cosα}$,
∴BM=$\frac{mcosα}{sin(α-β)}$,
又因为x=BM•cosβ=$\frac{mcosαcosβ}{sin(α-β)}$>n时没有触礁危险,
即mcosαcosβ>nsin(α-β),(1)正确;
$\frac{m}{n}>\frac{sin(α-β)}{cosαcosβ}$=tanα-tanβ,(3)正确.
故答案为:(1)(3).
点评 本题主要考查正弦定理的应用,考查学生利用数学知识解决实际问题的能力,属基础题.

练习册系列答案
相关题目
13.sin10°cos50°+cos10°sin50°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
20.已知{an}是等比数列,a1=1,a2=2,则a1a2+a2a3+…+anan+1=( )
| A. | $\frac{2}{3}$(1-4-n) | B. | $\frac{2}{3}$(1-2-n) | C. | $\frac{2}{3}$(4n-1) | D. | 2n+1-2 |
10.下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为$\widehaty$=0.8x-155,后因某未知原因第5组数据的y值模糊不清,此位置数据记为m(如表所示),则利用回归方程可求得实数m的值为( )
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A. | 8.3 | B. | 8.2 | C. | 8.1 | D. | 8 |
17.若方程x2+$\frac{{y}^{2}}{a}$=1(a是常数),则下列结论正确的是( )
| A. | 任意实数a方程表示椭圆 | B. | 存在实数a方程表示椭圆 | ||
| C. | 任意实数a方程表示双曲线 | D. | 存在实数a方程表示抛物线 |
 如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.
如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.