题目内容
15.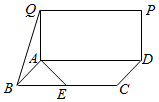 如图,四边形ABCD和ADPQ均为长方形,它们所在的平面互相垂直,且AB=AQ=$\frac{1}{2}$AD,E为BC的中点,则异面直线BQ与AE所成的角大小为60°.
如图,四边形ABCD和ADPQ均为长方形,它们所在的平面互相垂直,且AB=AQ=$\frac{1}{2}$AD,E为BC的中点,则异面直线BQ与AE所成的角大小为60°.
分析 以A为原点,AB为x轴,AD为y轴,AQ为z轴,建立空间直角坐标系,利用同量法能求出异面直线BQ与AE所成的角的大小.
解答  解:∵四边形ABCD和ADPQ均为长方形,它们所在的平面互相垂直,且AB=AQ=$\frac{1}{2}$AD,E为BC的中点,
解:∵四边形ABCD和ADPQ均为长方形,它们所在的平面互相垂直,且AB=AQ=$\frac{1}{2}$AD,E为BC的中点,
∴以A为原点,AB为x轴,AD为y轴,AQ为z轴,建立空间直角坐标系,
设AB=AQ=$\frac{1}{2}$AD=1,则B(1,0,0),Q(0,0,1),A(0,0,0),E(1,1,0),
$\overrightarrow{BQ}$=(-1,0,1),$\overrightarrow{AE}$=(1,1,0),
设异面直线BQ与AE所成的角为α,
则cosα=|cos<$\overrightarrow{BQ},\overrightarrow{AE}$>|=$\frac{|\overrightarrow{BQ}•\overrightarrow{AE}|}{|\overrightarrow{BQ}|•|\overrightarrow{AE}|}$=$\frac{1}{\sqrt{2}×\sqrt{2}}$=$\frac{1}{2}$,
∴α=60°.
∴异面直线BQ与AE所成的角为60°.
故答案为:60°.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
5.已知点A(0,1),B(3,2),C(a,0),若A,B,C三点共线,则a=( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | -2 | D. | -3 |
20.在△ABC中,若顶点B、C的坐标分别是(-a,0)和(a,0),其中a>0,G为△ABC的重心(三角形三条中线的交点),若|AG|=2,则点G的轨迹方程是( )
| A. | x2+y2=1(y≠0) | B. | x2+y2=4(y≠0) | C. | x2+y2=9(y≠0) | D. | x2+y2=a2(y≠0) |