在△ABC中.若顶点B.C的坐标分别是.其中a＞0.G为△ABC的重心.若|AG|=2.则点G的轨迹方程是( )A．x2+y2=1B．x2+y2=4C．x2+y2=9D．x2+y2=a2 题目和参考答案——青夏教育精英家教网——

题目内容

20．在△ABC中，若顶点B、C的坐标分别是（-a，0）和（a，0），其中a＞0，G为△ABC的重心（三角形三条中线的交点），若|AG|=2，则点G的轨迹方程是（　　）

A．

x²+y²=1（y≠0）

B．

x²+y²=4（y≠0）

C．

x²+y²=9（y≠0）

D．

x²+y²=a²（y≠0）

分析由题意，|OG|=1，即可得出结论．

解答解：由题意，|OG|=1，
设G（x，y）（y≠0），则x²+y²=1（y≠0），
故选：A．

点评本题考查轨迹方程，考查学生的计算能力，正确理解重心的概念是关键．

练习册系列答案

初中英语听力系列答案

单元测试卷齐鲁书社系列答案

中考导学案系列答案

中考大提速系列答案

中考专题通系列答案

中考第三轮复习冲刺专用模拟试卷系列答案

中考攻略中考及会考真题汇编系列答案

培优口算题卡系列答案

开心口算题卡系列答案

口算题卡河北少年儿童出版社系列答案

相关题目

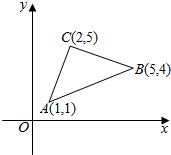如图，已知A（1，1），B（5，4），C（2，5），设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量．
（1）求单位向量$\overrightarrow{a}$的坐标；
（2）求向量$\overrightarrow{AC}$在向量$\overrightarrow{a}$上的投影；
（3）求△ABC的面积S_△ABC．

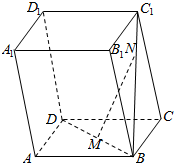如图所示，已知几何体ABCD-A₁B₁C₁D₁是平行六面体．
（1）化简$\frac{1}{2}$$\overrightarrow{A{A}_{1}}$+$\overrightarrow{BC}$+$\frac{2}{3}$$\overrightarrow{AB}$，并在图上标出结果；
（2）设M是底面ABCD的中心，N是侧面BCC₁B₁对角线BC₁上的点，且C₁N=$\frac{1}{4}$C₁B，设$\overrightarrow{MN}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$+γ$\overrightarrow{A{A}_{1}}$，求α，β，γ的值．

8．已知单调递增数列{a_n}满足a_n=3ⁿ-λ•2ⁿ（其中λ为常数，n∈N⁺），则实数λ的取值范围是λ＜3．

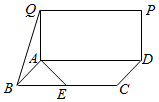如图，四边形ABCD和ADPQ均为长方形，它们所在的平面互相垂直，且AB=AQ=$\frac{1}{2}$AD，E为BC的中点，则异面直线BQ与AE所成的角大小为60°．

5．已知曲线E₁，E₂的极坐标方程分别为ρ=4cosθ，ρ•cos（θ-$\frac{π}{4}$）=4，绕极点将曲线E₁逆时针旋转角α，α∈（0，$\frac{π}{2}$），得到曲线E₃．
（1）当α=$\frac{π}{6}$时，求曲线E₃的极坐标方程；
（2）当E₃与E₂有且仅有一个公共点时，求α．

12．已知数列{a_n}满足log₃a_n+2=log₃a_n+1（n∈N^*）且a₂+a₄+a₆=9，则log${\;}_{\frac{1}{3}}$（a₅+a₇+a₉）的值是（　　）

9．已知命题P：f（x）=a^x-a^-x是增函数，命题q：?x∈（0，+∞）使x+$\frac{1}{x}$＞a，若p∨q为真，p∧q为假，求实数a的取值范围．

10．长方体ABCD-A₁B₁C₁D₁中，有三个面的面积分别为12，20，15，则其外接球球面上的点到平面ABCD的最大距离为（　　）

$\frac{2\sqrt{5}+5}{2}$

$\frac{2\sqrt{3}+3}{2}$

$\frac{5\sqrt{2}+5}{2}$