题目内容
7.若△ABC边BC,CA,AB上的高分别为ha、hb、hc,且ha:hb:hc=6:4:3,则tanC=-$\sqrt{15}$.分析 由已知设a=2k,b=3k,c=4k,k>0,利用余弦定理能求出cosC,由此能求出tanC.
解答 解:∵△ABC边BC,CA,AB上的高分别为ha、hb、hc,且ha:hb:hc=6:4:3,
$S△ABC=\frac{1}{2}a{h}_{a}=\frac{1}{2}b{h}_{b}=\frac{1}{2}c{h}_{c}$,
∴$a:b:c=\frac{1}{{h}_{a}}:\frac{1}{{h}_{b}}:\frac{1}{{h}_{c}}$=$\frac{1}{6}:\frac{1}{4}:\frac{1}{3}$=2:3:4,
设a=2k,b=3k,c=4k,k>0,
则cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{4{k}^{2}+9{k}^{2}-16{k}^{2}}{2×2k×3k}$=-$\frac{1}{4}$,
∴sinC=$\sqrt{1-\frac{1}{16}}$=$\frac{\sqrt{15}}{4}$,
tanC=$\frac{sinC}{cosC}$=$\frac{\frac{\sqrt{15}}{4}}{-\frac{1}{4}}$=-$\sqrt{15}$.
故答案为:-$\sqrt{15}$.
点评 本题考查正切函数的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
17.已知正项等比数列{an},其前n项和为Sn,ak-1=2,ak•ak+2=a${\;}_{5}^{2}$=64,则S10等于( )
| A. | 410-1 | B. | $\frac{{4}^{10}-1}{3}$ | C. | 210-1 | D. | $\frac{{2}^{10}-1}{2}$ |
18.幂函数的图象过点(5,$\sqrt{5}$),则它的单调递增区间是( )
| A. | [0,+∞) | B. | [-1,+∞) | C. | (-∞,+∞) | D. | (-∞,0) |
12.已知数列{an}满足log3an+2=log3an+1(n∈N*)且a2+a4+a6=9,则log${\;}_{\frac{1}{3}}$(a5+a7+a9)的值是( )
| A. | -8 | B. | -$\frac{1}{8}$ | C. | 8 | D. | $\frac{1}{8}$ |
19.已知变量x,y之间具有线性相关关系,其散点图如图所示,则其回归方程可能为( )
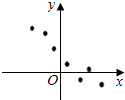

| A. | $\widehat{y}$=1.5x+2 | B. | $\widehat{y}$=-1.5x+2 | C. | $\widehat{y}$=1.5x-2 | D. | $\widehat{y}$=-1.5x-2 |
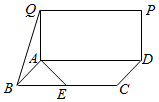 如图,四边形ABCD和ADPQ均为长方形,它们所在的平面互相垂直,且AB=AQ=$\frac{1}{2}$AD,E为BC的中点,则异面直线BQ与AE所成的角大小为60°.
如图,四边形ABCD和ADPQ均为长方形,它们所在的平面互相垂直,且AB=AQ=$\frac{1}{2}$AD,E为BC的中点,则异面直线BQ与AE所成的角大小为60°.