题目内容
(1)设数列{an}满足:a1=1,an+1=3an,n∈N+.求{an}的通项公式及前n项和Sn;
(2)已知数列{bn}的前n项和为Tn,且Tn=-n2+4n,求Tn的最大值和通项bn.
(2)已知数列{bn}的前n项和为Tn,且Tn=-n2+4n,求Tn的最大值和通项bn.
考点:等比数列的前n项和,数列的函数特性,等差数列的前n项和
专题:等差数列与等比数列
分析:(1)由题意和等比数列的定义判断出数列{an}是等比数列,代入通项公式、前n项和公式化简即可;
(2)将Tn=-n2+4n配方,由二次函数的性质求出最大值,再根据当n=1时b1=T1,当n≥2时bn=Tn-Tn-1,求出通项bn.
(2)将Tn=-n2+4n配方,由二次函数的性质求出最大值,再根据当n=1时b1=T1,当n≥2时bn=Tn-Tn-1,求出通项bn.
解答:
解:(1)由an+1=3an 得,
=3,
所以数列{an}是首项为1,公比为3的等比数列…2分
则an=1×3n-1=3n-1 4分,
Sn=
=
(3n-1) 6分
(2)由题意得,Tn=-n2+4n=-(n-2)2+4,8分
当n=2时,Tn取得最大值4 …9分
当n=1时,b1=T1=3 …9分
当n≥2时,bn=Tn-Tn-1=-n2+4n-[-(n-1)2+4(n-1)]=-2n+5 12分
且b1也适合上式,所以bn=-2n+5 13分.
| an+1 |
| an |
所以数列{an}是首项为1,公比为3的等比数列…2分
则an=1×3n-1=3n-1 4分,
Sn=
| 1-3n |
| 1-3 |
| 1 |
| 2 |
(2)由题意得,Tn=-n2+4n=-(n-2)2+4,8分
当n=2时,Tn取得最大值4 …9分
当n=1时,b1=T1=3 …9分
当n≥2时,bn=Tn-Tn-1=-n2+4n-[-(n-1)2+4(n-1)]=-2n+5 12分
且b1也适合上式,所以bn=-2n+5 13分.
点评:本题考查等比数列的定义、通项公式、前n项和公式,利用二次函数的性质求数列前n项和的最值问题,以及数列的通项与前n项和的关系式的应用,属于中档题.

练习册系列答案
相关题目
求适合下列条件的椭圆的标准方程:
(1)一条准线方程为y=
,离心率为
;
(2)与椭圆
+
=1有相同的焦点,且经过点(1,
);
(3)经过A(4,
),B(-3,-
)两点.
(1)一条准线方程为y=
| 9 |
| 2 |
| 2 |
| 3 |
(2)与椭圆
| x2 |
| 16 |
| y2 |
| 15 |
| 3 |
| 2 |
(3)经过A(4,
| 12 |
| 5 |
| 16 |
| 5 |
已知关于x的方程为
+x2=2x+
,则该方程实数解的个数是( )
| 1 |
| |x| |
| 3|x| |
| x |
| A、1 | B、2 | C、3 | D、4 |
已知△ABC中c=4,a=4
,C=30°,则A等于( )
| 3 |
| A、60° |
| B、60°或120° |
| C、30° |
| D、30°或150° |
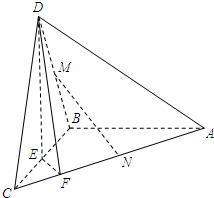 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,