题目内容
已知y=f(x+
)为偶函数,且当任意
≤x1<x2<+∞时,总有
<0,则下列关系式中一定成立的是( )
| 3 |
| 2 |
| 3 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
| A、f(3)<f(1)<f(π) |
| B、f(π)<f(0)<f(1) |
| C、f(0)<f(1)<f(2) |
| D、f(0)<f(π)<f(2) |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:先求出函数f(x)在(
,+∞)递减,再得出函数的关于x=
对称,从而判断出函数的大小.
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:∵任意
≤x1<x2<+∞时,总有
<0,则f(x)在(
,+∞)递减,
∵函数y=f(x+
)为偶函数,且此函数是由f(x)左移
个单位得到,
∴函数f(x)关于x=
对称,
∴函数在(-∞,
)递增,
如图示:
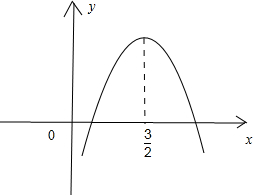
由图象的对称性知f(0)=f(3)、f(1)=f(2),
∵f(x)在(
,+∞)递减,
∴f(π)<f(3)<f(2),∴f(π)<f(0)<f(1)
故选:B.
| 3 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
| 3 |
| 2 |
∵函数y=f(x+
| 3 |
| 2 |
| 3 |
| 2 |
∴函数f(x)关于x=
| 3 |
| 2 |
∴函数在(-∞,
| 3 |
| 2 |
如图示:

由图象的对称性知f(0)=f(3)、f(1)=f(2),
∵f(x)在(
| 3 |
| 2 |
∴f(π)<f(3)<f(2),∴f(π)<f(0)<f(1)
故选:B.
点评:本题考查了函数的单调性,函数的对称性,函数的奇偶性,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知关于x的方程为
+x2=2x+
,则该方程实数解的个数是( )
| 1 |
| |x| |
| 3|x| |
| x |
| A、1 | B、2 | C、3 | D、4 |
已知关于x的方程为2kx2-2x-3k-2=0的两个实数根一个小于1,另一个大于1,则实数k的取值范围是( )
| A、k>0 |
| B、k<-4 |
| C、-4<k<0 |
| D、k<-4或k>0 |
已知a,b,c∈R,命题“若 a+b+c=1,则a2+b2+c2≤
”的否命题是( )
| 1 |
| 9 |
A、若a2+b2+c2≥1,则a+b+c=
| ||
B、若a+b+c=1,则a2+b2+c2<
| ||
C、若a+b+c≠1,则a2+b2+c2<
| ||
D、若a+b+c≠1,则a2+b2+c2>
|
已知函数y=lg[(a2-1)x2-2(a-1)x+3]的值域为R,则实数a的取值范围是( )
| A、[-2,1] |
| B、[-2,-1] |
| C、(-2,1) |
| D、(-∞,-2)∪[1,+∞) |
“m=1”是“直线mx+y+2=0与直线x+my-1=0相互平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |