题目内容
20.下列命题中,真命题是( )| A. | 存在x<0,使得2x>1 | |
| B. | 对任意x∈R,x2-x+l>0 | |
| C. | “x>l”是“x>2”的充分不必要条件 | |
| D. | “P或q是假命题”是“非p为真命题”的必要而不充分条件 |
分析 分别对各个选项进行判断即可.
解答 解:对于A:x<0时,2x<0,故A错误;
对于B:x2-x+l=${(x-\frac{1}{2})}^{2}$+$\frac{3}{4}$>0,故B正确;
对于C:“x>l”是“x>2”的必要不充分条件,故C错误;
对于D:P或q是假命题”是“非p为真命题”的充分不必要条件,故D错误;
故选:B.
点评 本题考查了命题的真假,考查充分必要条件,是一道基础题.

练习册系列答案
相关题目
15.若函数f(x)=sin(2x+φ)(0<φ<π)的图象关于直线x=$\frac{π}{6}$对称,则φ的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
5.已知sinφ=$\frac{3}{5}$,且φ∈($\frac{π}{2}$,π),函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$,则f($\frac{π}{4}$)的值为( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12.已知圆O:x2+y2=4上到直线l:x+y=a的距离等于1的点至少有2个,则a的取值范围为( )
| A. | (-3$\sqrt{2}$,3$\sqrt{2}$) | B. | (-∞,-3$\sqrt{2}$)∪(3$\sqrt{2}$,+∞) | C. | (-2$\sqrt{2}$,2$\sqrt{2}$) | D. | [-3$\sqrt{2}$,3$\sqrt{2}$] |
10.已知直线y=k(x-1)及抛物线y2=2x,则( )
| A. | 直线与抛物线有且只有一个公共点 | B. | 直线与抛物线有两个公共点 | ||
| C. | 直线与抛物线有一个或两个公共点 | D. | 直线与抛物线可能没有公共点 |
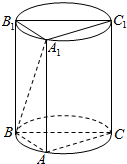 如图,四边形BCC1B1是圆柱的轴截面.AA1是圆柱的一条母线,已知AB=4,AC=2$\sqrt{2}$,AA1=3.
如图,四边形BCC1B1是圆柱的轴截面.AA1是圆柱的一条母线,已知AB=4,AC=2$\sqrt{2}$,AA1=3.