题目内容
12.已知圆O:x2+y2=4上到直线l:x+y=a的距离等于1的点至少有2个,则a的取值范围为( )| A. | (-3$\sqrt{2}$,3$\sqrt{2}$) | B. | (-∞,-3$\sqrt{2}$)∪(3$\sqrt{2}$,+∞) | C. | (-2$\sqrt{2}$,2$\sqrt{2}$) | D. | [-3$\sqrt{2}$,3$\sqrt{2}$] |
分析 由题意可得圆心(0,0)到直线l:x+y=a的距离d满足d<r+1,根据点到直线的距离公式求出d,再解绝对值不等式求得实数a的取值范围.
解答 解:由圆的方程可知圆心为(0,0),半径为2.
因为圆上的点到直线l的距离等于1的点至少有2个,所以圆心到直线l的距离d<r+1=3,
即d=$\frac{|-a|}{\sqrt{2}}$<3,解得-3$\sqrt{2}$<a<3$\sqrt{2}$.
故选:A.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式,绝对值不等式的解法,属于基础题.

练习册系列答案
相关题目
2.过抛物线x2=4y的焦点任作一直线l交抛物线于M,N两点,O为坐标原点,则△MON的面积的最小值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
20.下列命题中,真命题是( )
| A. | 存在x<0,使得2x>1 | |
| B. | 对任意x∈R,x2-x+l>0 | |
| C. | “x>l”是“x>2”的充分不必要条件 | |
| D. | “P或q是假命题”是“非p为真命题”的必要而不充分条件 |
17.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(3,m),若向量$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为3,则实数m=( )
| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -3$\sqrt{3}$ |
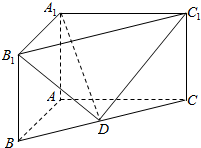 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点,求直线DB1与平面A1C1D所成角的正弦值.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点,求直线DB1与平面A1C1D所成角的正弦值.