题目内容
10．已知直线y=k（x-1）及抛物线y2=2x，则（ ）| A． | 直线与抛物线有且只有一个公共点 | B． | 直线与抛物线有两个公共点 | ||
| C． | 直线与抛物线有一个或两个公共点 | D． | 直线与抛物线可能没有公共点 |
分析 把直线y=kx-k代入抛物线y2=8x，分类讨论，即可得出结论．
解答 解：联立直线y=k（x-1）及抛物线y2=2x，k2x2-（2k2+2）x+k2=0，
k=0时，x=0，∴y=0，∴直线与抛物线有一个公共点；
k≠0时，△=（2k2+2）2-4k4=8k2+4＞0，
∴直线与抛物线有两个公共点．
故选：C．
点评 本题考查直线与抛物线的位置关系，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
20．下列命题中，真命题是（ ）
| A． | 存在x＜0，使得2x＞1 | |
| B． | 对任意x∈R，x2-x+l＞0 | |
| C． | “x＞l”是“x＞2”的充分不必要条件 | |
| D． | “P或q是假命题”是“非p为真命题”的必要而不充分条件 |
18．在复平面内，复数$\frac{2}{1-i}$-2对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
5．长方体ABCD-A1B1C1D1中，AA1=3，AD=4，AB=5，则直线BD1与平面ABCD所成的角的正弦值是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{{3\sqrt{2}}}{10}$ | C． | $\frac{3}{{\sqrt{34}}}$ | D． | $\frac{5}{{\sqrt{34}}}$ |
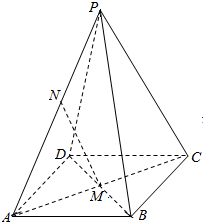（理科做）如图，正四棱锥P-ABCD中，PA=BD，点M为AC，BD的交点，点N为AP中点．
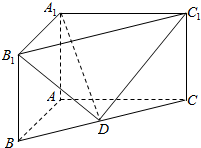如图，在直三棱柱ABC-A1B1C1中，AB⊥AC，AB=2，AC=4，AA1=3，D是BC的中点，求直线DB1与平面A1C1D所成角的正弦值．