题目内容
5.已知sinφ=$\frac{3}{5}$,且φ∈($\frac{π}{2}$,π),函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$,则f($\frac{π}{4}$)的值为( )| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 由周期求出ω,由条件求出cosφ的值,从而求得f($\frac{π}{4}$)的值.
解答 解:根据函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$,
可得$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{π}{2}$,∴ω=2.
由sinφ=$\frac{3}{5}$,且φ∈($\frac{π}{2}$,π),可得 cosφ=-$\frac{4}{5}$,
∴则f($\frac{π}{4}$)=sin($\frac{π}{2}$+φ)=cosφ=-$\frac{4}{5}$,
故选:B.
点评 本题主要考查正弦函数的周期性,同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
15.已知集合P={x|1<2x<2},Q={x|log${\;}_{\frac{1}{2}}$x>1},则P∩Q=( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2},1$) | C. | (-1,$\frac{1}{2}$) | D. | (0,1) |
20.下列命题中,真命题是( )
| A. | 存在x<0,使得2x>1 | |
| B. | 对任意x∈R,x2-x+l>0 | |
| C. | “x>l”是“x>2”的充分不必要条件 | |
| D. | “P或q是假命题”是“非p为真命题”的必要而不充分条件 |
10.已知集合M={5,a2-3a+5},N={1,3},若M∩N≠∅,则实数a的值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 1或2 |
17.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(3,m),若向量$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为3,则实数m=( )
| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -3$\sqrt{3}$ |
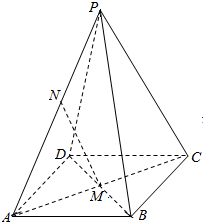 (理科做)如图,正四棱锥P-ABCD中,PA=BD,点M为AC,BD的交点,点N为AP中点.
(理科做)如图,正四棱锥P-ABCD中,PA=BD,点M为AC,BD的交点,点N为AP中点.