题目内容
11.若函数f(x)=ax(a>0且a≠1)的反函数的图象过点(3,-1),则a=$\frac{1}{3}$.分析 利用互为反函数的性质即可得出.
解答 解:∵函数f(x)=ax(a>0且a≠1)的反函数的图象过点(3,-1),
∴3=a-1,
解得a=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了互为反函数的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.过抛物线x2=4y的焦点任作一直线l交抛物线于M,N两点,O为坐标原点,则△MON的面积的最小值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
6.已知抛物线y2=4x的焦点为F,A、B为抛物线上两点,若$\overrightarrow{AF}=3\overrightarrow{FB}$,O为坐标原点,则△AOB的面积为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
20.下列命题中,真命题是( )
| A. | 存在x<0,使得2x>1 | |
| B. | 对任意x∈R,x2-x+l>0 | |
| C. | “x>l”是“x>2”的充分不必要条件 | |
| D. | “P或q是假命题”是“非p为真命题”的必要而不充分条件 |
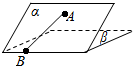 如图,二面角α-l-β的大小是30°,线段AB?α,B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是$\frac{1}{4}$.
如图,二面角α-l-β的大小是30°,线段AB?α,B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是$\frac{1}{4}$.