题目内容
5.已知数列{an}是以m为首项,m为公差的等差数列,数列{bn}是以m为首项,m为公比的等比数列,其中a2=b2,设Sn是数列{bn}的前n项和,则数列$\left\{{\frac{{4{b_n}}}{{{S_n}{S_{n+1}}}}}\right\}$的前n项和为1-$\frac{1}{{2}^{n+1}-1}$.分析 由题意可得:an=mn,bn=mn.其中a2=b2,可得2m=m2,m≠0,解得m.可得bn=2n,数列{bn}的前n项和Sn,再利用“裂项求和”方法即可得出.
解答 解:由题意可得:an=m+m(n-1)=mn,bn=m×mn-1=mn.
其中a2=b2,∴2m=m2,m≠0,解得m=2.
∴bn=2n.
∴数列{bn}的前n项和Sn=$\frac{2({2}^{n}-1)}{2-1}$=2n+1-2,
∴$\frac{4{b}_{n}}{{S}_{n}{S}_{n+1}}$=$\frac{4×{2}^{n}}{({2}^{n+1}-2)({2}^{n+2}-2)}$=$\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$.
∴数列$\left\{{\frac{{4{b_n}}}{{{S_n}{S_{n+1}}}}}\right\}$的前n项和为=$\frac{1}{{2}^{1}-1}$-$\frac{1}{{2}^{n+1}-1}$=1-$\frac{1}{{2}^{n+1}-1}$.
故答案为:1-$\frac{1}{{2}^{n+1}-1}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.某班有男、女优秀少先队员各2名,现需选出2名优秀少先队员到社区做公益宣传活动,则选出的两名队员性别相同的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
14.设命题p:?x∈(0,+∞),$\sqrt{x}$≥log2x,则¬p为( )
| A. | ?x∈(0,+∞),$\sqrt{x}$≥log2x | B. | ?x∈(0,+∞),$\sqrt{x}$<log2x | C. | ?x∈(0,+∞),$\sqrt{x}$=log2x | D. | ?x∈(0,+∞),$\sqrt{x}$<log2x |
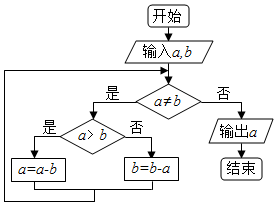 上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )
上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )