题目内容
如图，矩形OABC在变换T的作用下变成了平行四边形OA′B′C′，变换T所对应的矩阵为M，矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍，纵坐标伸长到原来的3倍所对应的变换矩阵． （Ⅰ）求（MN）-1；
（Ⅱ）判断矩阵MN是否存在特征值．
考点：特征值与特征向量的计算,变换、矩阵的相等,矩阵变换的性质
专题：选作题,矩阵和变换
分析：（Ⅰ）利用待定系数法，求出矩阵M、N，可得MN，再求（MN）-1；
（Ⅱ）求出矩阵MN的特征多项式，可得△＜0，即可得出结论．
（Ⅱ）求出矩阵MN的特征多项式，可得△＜0，即可得出结论．
解答：
解：（Ⅰ）设M=
，则由题意，可得
=
，
=
，
解得a=0，b=-1，c=1，d=1，
∴M=
，N=
，
∴MN=
=
，
∴（MN）-1=
；
（Ⅱ）矩阵MN的特征多项式f（λ）=
=λ2-3λ+6=0，
∵△＜0，
∴矩阵MN不存在特征值．
|
|
|
|
|
|
|
解得a=0，b=-1，c=1，d=1，
∴M=
|
|
∴MN=
|
|
|
∴（MN）-1=
|
（Ⅱ）矩阵MN的特征多项式f（λ）=
|
∵△＜0，
∴矩阵MN不存在特征值．
点评：本题考查了矩阵特征值与特征向量的计算等基础知识，属于基础题．
练习册系列答案
相关题目
已知点D是△ABC的边BC上的中点，且|
|=4，|
|=2，则
•
=（ ）
| AC |
| AB |
| AD |
| BC |
| A、2 | ||
| B、4 | ||
| C、6 | ||
D、2
|
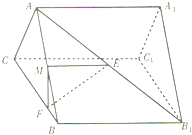如图，直三棱柱（侧棱垂直于底面的三棱柱）ABC-A1B1C1的各棱长都相等，M、E分别是AB和AB1的中点，点F在BC上，且满足BF=1，FC=3．
在正三棱柱ABC-A1B1C1 中，AB=2，AA1=1，D是BC的中点，点P在平面BCC1B1内，PB1=PC1=