题目内容
化简、求值：
（1）已知tanα=2，求值：4sin2α-3sinαcosα-5cos2α．
（2）求值：
-sin10°（tan-15°-tan5°）．
（1）已知tanα=2，求值：4sin2α-3sinαcosα-5cos2α．
（2）求值：
| 1+cos20° |
| 2sin20° |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）由条件利用同角三角函数的基本关系把要求的式子化为
，从而求得结果．
（2）由条件利用同角三角函数的基本关系把要求的式子化为
-2cos10°，通分后利用诱导公式、和差化积公式化为cos30°，从而得到结果．
| 4tan2α-3tanα-5 |
| tan2α+1 |
（2）由条件利用同角三角函数的基本关系把要求的式子化为
| cos10° |
| 2sin10° |
解答：
解：（1）∵已知tanα=2，∴4sin2α-3sinαcosα-5cos2α=
=
=
=-
．
（2）
-sin10°（tan-15°-tan5°）=
-sin10°（
-
）
=
-sin10°•
=
-2cos10°=
-2cos10°
=
=
=
=
=
=
=cos30°=
．
| 4sin2α-3sinαcosα-5cos2α |
| sin2α+cos2α |
=
| 4tan2α-3tanα-5 |
| tan2α+1 |
| 16-12-5 |
| 4+1 |
| 1 |
| 5 |
（2）
| 1+cos20° |
| 2sin20° |
| 1+cos20° |
| 2sin20° |
| cos5° |
| sin5° |
| sin5° |
| cos5° |
=
| 1+cos20° |
| 2sin20° |
| cos10° | ||
|
| 1+2cos210°-1 |
| 4sin10°cos10° |
| cos10° |
| 2sin10° |
=
| cos10°-4sin10°cos10° |
| 2sin10° |
| sin80°-2sin20° |
| 2sin10° |
| sin80°-sin20°-sin20° |
| 2sin10° |
=
| 2cos50°sin30°-sin20° |
| 2sin10° |
| sin40°-sin20° |
| 2sin10° |
| 2cos30°sin10° |
| 2sin10° |
| ||
| 2 |
点评：本题主要考查同角三角函数的基本关系、诱导公式、和差化积公式的应用，属于中档题．
练习册系列答案
相关题目
已知向量
、
的夹角为45°，且|
|=1，|2
-
|=
，则|
|=（ ）
| a |
| b |
| a |
| a |
| b |
| 10 |
| b |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=∠ADC=90°，∠BAD=120°，AD=AB=1，AC交BD于O点．
如图，矩形OABC在变换T的作用下变成了平行四边形OA′B′C′，变换T所对应的矩阵为M，矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍，纵坐标伸长到原来的3倍所对应的变换矩阵．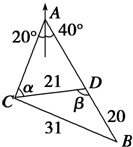 
C位于A城的南偏西20°的位置，B位于A城的南偏东40°的位置，有一人距C为31千米的B处正沿公路向A城走去，走了20千米后到达D处，此时CD间的距离为21千米，问这人还要走多少千米才能到达A城？