题目内容
 在正三棱柱ABC-A1B1C1 中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=
在正三棱柱ABC-A1B1C1 中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=| 2 |
考点:二面角的平面角及求法
专题:空间角
分析:由已知条件推导出∠C1DC是二面角C1-AD-C的平面角,由此能求出二面角C1-AD-C的大小.
解答:
解:∵正三棱柱ABC-A1B1C1 中,
AB=2,AA1=1,D是BC的中点,
∴AD⊥CD,CC1⊥CD,CC1⊥AC,
∴AC1=
=
,
AD=
=
,C1D=
=
,
∴AD⊥C1D,
∴∠C1DC是二面角C1-AD-C的平面角,
∵tan∠C1DC=
=1,∴∠C1DC=45°,
∴二面角C1-AD-C的大小为45°.
AB=2,AA1=1,D是BC的中点,
∴AD⊥CD,CC1⊥CD,CC1⊥AC,
∴AC1=
| 22+12 |
| 5 |
AD=
| 22-12 |
| 3 |
| 1+1 |
| 2 |
∴AD⊥C1D,
∴∠C1DC是二面角C1-AD-C的平面角,
∵tan∠C1DC=
| C1C |
| DC |
∴二面角C1-AD-C的大小为45°.
点评:本题考查二面角的大小的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点. 如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵.
如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵. 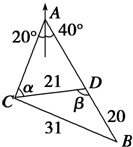 C位于A城的南偏西20°的位置,B位于A城的南偏东40°的位置,有一人距C为31千米的B处正沿公路向A城走去,走了20千米后到达D处,此时CD间的距离为21千米,问这人还要走多少千米才能到达A城?
C位于A城的南偏西20°的位置,B位于A城的南偏东40°的位置,有一人距C为31千米的B处正沿公路向A城走去,走了20千米后到达D处,此时CD间的距离为21千米,问这人还要走多少千米才能到达A城?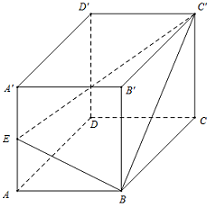 已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值.
已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值.