题目内容
已知函数f(x)=x•lnx,g(x)=ax3-
x-
.
(1)求f(x)的单调增区间和最小值;
(2)若函数y=f(x)与函数y=g(x)在交点处存在公共切线,求实数a的值;
(3)若x∈(0,e2]时,函数y=f(x)的图象恰好位于两条平行直线l1:y=kx;l2:y=kx+m之间,当l1与l2间的距离最小时,求实数m的值.
| 1 |
| 2 |
| 2 |
| 3e |
(1)求f(x)的单调增区间和最小值;
(2)若函数y=f(x)与函数y=g(x)在交点处存在公共切线,求实数a的值;
(3)若x∈(0,e2]时,函数y=f(x)的图象恰好位于两条平行直线l1:y=kx;l2:y=kx+m之间,当l1与l2间的距离最小时,求实数m的值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,导数的概念及应用,导数的综合应用,直线与圆
分析:(1)求出f(x)的导数,求得单调区间和极值,也为最值;
(2)分别求出导数,设公切点处的横坐标为x°,分别求出切线方程,再联立解方程,即可得到a;
(3)求出两直线的距离,再令h(x)=xlnx-(lnx°+1)x-x°,求出导数,运用单调性即可得到最小值,进而说明当d最小时,x°=e,m=-e.
(2)分别求出导数,设公切点处的横坐标为x°,分别求出切线方程,再联立解方程,即可得到a;
(3)求出两直线的距离,再令h(x)=xlnx-(lnx°+1)x-x°,求出导数,运用单调性即可得到最小值,进而说明当d最小时,x°=e,m=-e.
解答:
解:(1)因为f'(x)=lnx+1,由f'(x)>0,得x>
,
所以f(x)的单调增区间为(
,+∞),
又当x∈(0,
)时,f'(x)<0,则f(x)在(0,
)上单调减,
当x∈(
,+∞)时,f'(x)>0,则f(x)在(
,+∞)上单调增,
所以f(x)的最小值为f(
)=-
.
(2)因为f'(x)=lnx+1,g′(x)=3ax2-
,
设公切点处的横坐标为x°,
则与f(x)相切的直线方程为:y=(lnx°+1)x-x°,
与g(x)相切的直线方程为:y=(3ax°2-
)x-2ax°3-
,
所以
,
解之得x°lnx°=-
,
由(1)知x°=
,所以a=
.
(3)若直线l1过(e2,2e2),则k=2,此时有lnx°+1=2(x°为切点处的横坐标),
所以x°=e,m=-e,
当k>2时,有l2:y=(lnx°+1)x-x°,l1:y=(lnx°+1)x,且x°>2,
所以两平行线间的距离d=
,
令h(x)=xlnx-(lnx°+1)x+x°,因为h'(x)=lnx+1-lnx°-1=lnx-lnx°,
所以当x<x°时,h'(x)<0,则h(x)在(0,x°)上单调减;
当x>x°时,h'(x)>0,则h(x)在(x°,e2)上单调增,
所以h(x)有最小值h(x°)=0,即函数f(x)的图象均在l2的上方,
令t(x)=
,
则t′(x)=
=
>0,
所以当x>x°时,t(x)>t(x°),
所以当d最小时,x°=e,m=-e.
| 1 |
| e |
所以f(x)的单调增区间为(
| 1 |
| e |
又当x∈(0,
| 1 |
| e |
| 1 |
| e |
当x∈(
| 1 |
| e |
| 1 |
| e |
所以f(x)的最小值为f(
| 1 |
| e |
| 1 |
| e |
(2)因为f'(x)=lnx+1,g′(x)=3ax2-
| 1 |
| 2 |
设公切点处的横坐标为x°,
则与f(x)相切的直线方程为:y=(lnx°+1)x-x°,
与g(x)相切的直线方程为:y=(3ax°2-
| 1 |
| 2 |
| 2 |
| 3e |
所以
|
解之得x°lnx°=-
| 1 |
| e |
由(1)知x°=
| 1 |
| e |
| e2 |
| 6 |
(3)若直线l1过(e2,2e2),则k=2,此时有lnx°+1=2(x°为切点处的横坐标),
所以x°=e,m=-e,
当k>2时,有l2:y=(lnx°+1)x-x°,l1:y=(lnx°+1)x,且x°>2,
所以两平行线间的距离d=
| x° | ||
|
令h(x)=xlnx-(lnx°+1)x+x°,因为h'(x)=lnx+1-lnx°-1=lnx-lnx°,
所以当x<x°时,h'(x)<0,则h(x)在(0,x°)上单调减;
当x>x°时,h'(x)>0,则h(x)在(x°,e2)上单调增,
所以h(x)有最小值h(x°)=0,即函数f(x)的图象均在l2的上方,
令t(x)=
| x2 |
| ln2x+2lnx+2 |
则t′(x)=
| 2xln2x+4xlnx+4x-2xlnx-2x |
| (ln2x+2lnx+2)2 |
| 2xln2x+2xlnx+2x |
| (ln2x+2lnx+2)2 |
所以当x>x°时,t(x)>t(x°),
所以当d最小时,x°=e,m=-e.
点评:本题考查导数的运用:求切线方程、求单调区间和极值、最值,考查两直线的距离和构造函数运用导数判断单调性,再运用求最值,考查运算能力,属于中档题和易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=3lnx+x2-
x+
在点(
,f(
))处的切线斜率是( )
| 3 |
| 3 |
| 3 |
| 3 |
A、-2
| ||
B、
| ||
C、2
| ||
D、4
|
若函数f(x)为定义在R上的奇函数,且在(0,+∞)内是增加的,又f(3)=0,则不等式
<0的解集为( )
| f(x)-f(-x) |
| x |
| A、(-3,0)∪(3,+∞) |
| B、(-3,0)∪(0,3) |
| C、(-∞,-3)∪(3,+∞) |
| D、(-∞,-3)∪(0,3) |
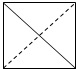
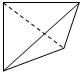
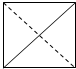
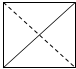 在空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,0),(1,0,1),(1,1,0),(0,1,1),且该四面体的俯视图如图,则左视图为( )
在空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,0),(1,0,1),(1,1,0),(0,1,1),且该四面体的俯视图如图,则左视图为( )
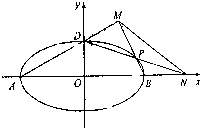 已知椭圆
已知椭圆 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.