题目内容
函数f(x)=3lnx+x2-
x+
在点(
,f(
))处的切线斜率是( )
| 3 |
| 3 |
| 3 |
| 3 |
A、-2
| ||
B、
| ||
C、2
| ||
D、4
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:求出原函数的导函数,然后直接取x=
得f(x)=3lnx+x2-
x+
在点(
,f(
))处的导数值,即切线的斜率.
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答:
解:由f(x)=3lnx+x2-
x+
得f′(x)=
+2x-
,
∴y′|x=
=2
.
故选:C.
| 3 |
| 3 |
| 3 |
| x |
| 3 |
∴y′|x=
| 3 |
| 3 |
故选:C.
点评:本题考查利用导数研究曲线上某点处的切线的斜率,求出函数在该点处的导数值是关键,是基础题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、棱柱的底面一定是平行四边形 |
| B、棱锥被平面分成的两部分不可能都是棱锥 |
| C、圆台平行于底面的截面是圆面 |
| D、半圆绕其直径所在直线旋转一周形成球 |
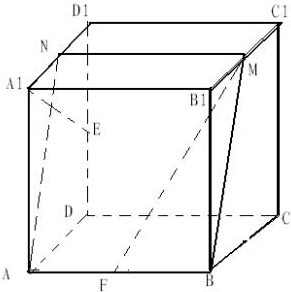 如图,在正方体ABCD-A1B1C1D1中,M,N,E,F,F分别是棱B1C1,A1D1,D1D,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,M,N,E,F,F分别是棱B1C1,A1D1,D1D,AB的中点.