题目内容
在面积为4cm2的扇形中,扇形周长的最小值为 cm.
考点:扇形面积公式
专题:计算题,三角函数的求值
分析:设半径为r,弧长为l,则
lr=4,扇形周长为l+2r≥2
,即可求出扇形周长的最小值.
| 1 |
| 2 |
| 2lr |
解答:
解:设半径为r,弧长为l,则
lr=4,
∴lr=8,
∴扇形周长为l+2r≥2
=8,
当且仅当l=2r时,扇形周长的最小值为8cm.
故答案为为:8.
| 1 |
| 2 |
∴lr=8,
∴扇形周长为l+2r≥2
| 2lr |
当且仅当l=2r时,扇形周长的最小值为8cm.
故答案为为:8.
点评:本题考查扇形的周长与面积,考查基本不等式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一个简单组合体的三视图及尺寸如图所示(单位:cm),该组合体的体积为( )
一个简单组合体的三视图及尺寸如图所示(单位:cm),该组合体的体积为( )| A、42cm3 |
| B、48cm3 |
| C、56cm3 |
| D、44cm3 |
 如图,平面ABB1A1为圆柱OO1的轴截面,点C为
如图,平面ABB1A1为圆柱OO1的轴截面,点C为

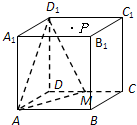 如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为
如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为