一个四棱锥的三视图如图所示.则该四棱锥的体积为( )A．$\frac{1}{6}$B．$\frac{1}{4}$C．$\frac{1}{3}$D．$\frac{1}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

18．

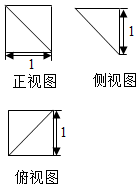一个四棱锥的三视图如图所示，则该四棱锥的体积为（　　）

A．

$\frac{1}{6}$

B．

$\frac{1}{4}$

C．

$\frac{1}{3}$

D．

$\frac{1}{2}$

分析由三视图可知，几何体是三棱柱割去一个同底等高的三棱锥所得，因此求几何体的体积．

解答解：由三视图可知，几何体是底面为直角边为1的等腰直角三角形，高为1的三棱柱割去一个同底等高的三棱锥所得，所以体积为$\frac{1}{2}×1×1×1-\frac{1}{3}×\frac{1}{2}×1×1×1=\frac{1}{3}$；
故选B．

点评本题考查了三视图对应几何体的体积计算；关键是正确还原几何体．

练习册系列答案

天舟文化精彩寒假团结出版社系列答案

哈皮寒假合肥工业大学出版社系列答案

寒假作业接力出版社系列答案

快乐假期寒假作业内蒙古人民出版社系列答案

快乐假期寒假作业新疆人民出版社系列答案

导学导思导练寒假评测新疆科学技术出版社系列答案

10．已知α，β是空间中两个不同的平面，m为平面β内的一条直线，则“α⊥β”是“m⊥α”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

6．已知A，B是椭圆C：$\frac{{x}^{2}}{2n}$+$\frac{{y}^{2}}{n}$=1（n＞0）的左、右顶点，动点M满足MB⊥AB，连接AM交椭圆于点P，记直线OM，PB的斜率分别为k₁，k₂，则k₁•k₂=-1．

13．复数z满足z（2-i）=3+i，则$\overline z$=（　　）

3．设数列{a_n}的前n项和为S_n，已知a₁=3，S_n+1=3S_n+3（n∈N^*），
（1）求数列{a_n}的通项公式；
（2）若b_n=$\frac{n}{{{a_{n+1}}-{a_n}}}$，求数列{b_n}的前n项和为T_n，n∈N^*．

10．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点与抛物线y²=2px（p＞0）的焦点重合，若抛物线的准线交双曲线于A、B两点，当|AB|=4a时，此双曲线的离心率为（　　）

7．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：|$\overrightarrow{a}$|=2，向量$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$夹角为$\frac{2π}{3}$，则$\overrightarrow{a}$$•\overrightarrow{b}$的取值范围是$[2-\frac{4\sqrt{3}}{3}，2+\frac{4\sqrt{3}}{3}]$．

7．已知双曲线$\frac{{x}^{2}}{3}$-y²=1，过右焦点向其渐近线作垂线，与两条渐近线分别交于A，B两点，O为坐标原点，则三角形AOB的面积是（　　）

A．

$\frac{3}{2}$

B．

$\frac{3\sqrt{3}}{2}$

试题分类