题目内容
10.已知α,β是空间中两个不同的平面,m为平面β内的一条直线,则“α⊥β”是“m⊥α”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 利用充分条件和必要条件的定义进行判断.
解答 解:由平面与平面垂直的判定定理知如果m为平面β内的一条直线,且m⊥α,则α⊥β,反之,α⊥β时,若m平行于α和β的交线,则m∥α,所以不一定能得到m⊥α,
所以“α⊥β”是“m⊥α”的必要不充分条件.
故选B.
点评 本题考查线面垂直、面面垂直问题以及充要条件问题,属基本题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
18.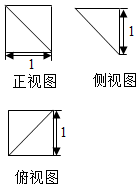 一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
 一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
一个四棱锥的三视图如图所示,则该四棱锥的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
18.已知点P在△ABC内(不含边界),且$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则$\frac{y+1}{x+2}$的取值范围为( )
| A. | ($\frac{1}{3}$,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{2}{3}$,1) | D. | ($\frac{1}{2}$,$\frac{2}{3}$) |
 如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为
如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为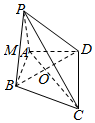 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点. 如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$
如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$