题目内容
7.已知双曲线$\frac{{x}^{2}}{3}$-y2=1,过右焦点向其渐近线作垂线,与两条渐近线分别交于A,B两点,O为坐标原点,则三角形AOB的面积是( )| A. | $\frac{3}{2}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
分析 求得双曲线的a,b,c和渐近线方程,运用点到直线的距离公式可得右焦点F到垂足A的距离为1,以及OA的长,运用正切函数的定义可得AB的长,再由三角形的面积公式计算即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{3}$-y2=1的a=$\sqrt{3}$,b=1,
c=$\sqrt{{a}^{2}+{b}^{2}}$=2,
渐近线方程为y=±$\frac{\sqrt{3}}{3}$x,
右焦点F(2,0)到渐近线y=$\frac{\sqrt{3}}{3}$x的距离为
|AF|=$\frac{\frac{2\sqrt{3}}{3}}{\sqrt{1+\frac{1}{3}}}$=1,
可设|FA|=1,可得|OA|=$\sqrt{|OF{|}^{2}-|AF{|}^{2}}$=$\sqrt{3}$,
由∠AOB=60°,可得|AB|=$\sqrt{3}$tan60°=3,
则△AOB的面积为S=$\frac{1}{2}$×3×$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$.
故选:B.
点评 本题考查双曲线的方程和性质,主要是渐近线方程的运用,考查点到直线的距离公式,以及运算能力,属于中档题.

练习册系列答案
相关题目
18.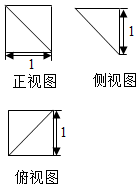 一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
 一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
一个四棱锥的三视图如图所示,则该四棱锥的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
18.已知点P在△ABC内(不含边界),且$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则$\frac{y+1}{x+2}$的取值范围为( )
| A. | ($\frac{1}{3}$,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{2}{3}$,1) | D. | ($\frac{1}{2}$,$\frac{2}{3}$) |
2.在△ABC中,角A、B、C的对边分别为a、b、c,且满足(b-a)sinA=(b-c)(sinB+sinC),则角C等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
13.函数f(x)=$\frac{1}{3}$x3-ax2-3a2x-4在(3,+∞)上是增函数,则实数a的取值范围是( )
| A. | a≥0 | B. | a≥1 | C. | a≤-3或a≥1 | D. | -3≤a≤1 |
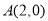 的直线
的直线 与
与 轴交于点
轴交于点 ,
,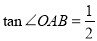 ,直线
,直线 位于
位于 轴左侧,且到
轴左侧,且到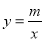 的图象经过点
的图象经过点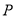 ,求
,求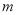 的值.
的值.