题目内容
6.已知A,B是椭圆C:$\frac{{x}^{2}}{2n}$+$\frac{{y}^{2}}{n}$=1(n>0)的左、右顶点,动点M满足MB⊥AB,连接AM交椭圆于点P,记直线OM,PB的斜率分别为k1,k2,则k1•k2=-1.分析 由题意可得A(-$\sqrt{2n}$,0),B($\sqrt{2n}$,0),M($\sqrt{2n}$,t),直线AM的方程为y=$\frac{t}{2\sqrt{2n}}$(x+$\sqrt{2n}$),代入椭圆方程,运用韦达定理可得P的坐标,再由直线的斜率公式,化简整理可得所求之积.
解答 解:由题意可得A(-$\sqrt{2n}$,0),B($\sqrt{2n}$,0),M($\sqrt{2n}$,t),
直线AM的方程为y=$\frac{t}{2\sqrt{2n}}$(x+$\sqrt{2n}$),
代入椭圆方程x2+2y2=2n,可得(1+$\frac{{t}^{2}}{4n}$)x2+$\frac{{t}^{2}}{\sqrt{2n}}$x+$\frac{{t}^{2}-4n}{2}$=0,
由-$\sqrt{2n}$•xP=$\frac{2n({t}^{2}-4n)}{{t}^{2}+4n}$,
解得xP=$\frac{\sqrt{2n}(4n-{t}^{2})}{4n+{t}^{2}}$,yP=$\frac{4nt}{4n+{t}^{2}}$,
即有k1k2=$\frac{t}{\sqrt{2n}}$•$\frac{{y}_{P}}{{x}_{P}-\sqrt{2n}}$=$\frac{t}{\sqrt{2n}}$•$\frac{4nt}{-2\sqrt{2n}{t}^{2}}$
=$\frac{t}{\sqrt{2n}}$•$\frac{\sqrt{2n}}{-t}$=-1.
故答案为:-1.
点评 本题考查椭圆的方程和性质,主要考查直线方程和椭圆方程联立,运用韦达定理,同时考查直线的斜率公式,化简整理的运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知集合A={x|y=x2+1},B={y|y=x2+1},则下列关系正确的是( )
| A. | A∩B=∅ | B. | A∩B=A | C. | A=B | D. | A∩B=B |
18.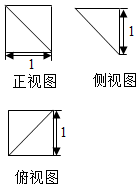 一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
 一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
一个四棱锥的三视图如图所示,则该四棱锥的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
 如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$
如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$