题目内容
14.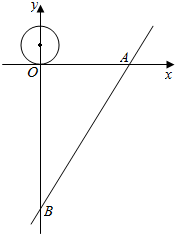 如图,在平面直角坐标系中,直线AB交x、y轴于点A(10$\sqrt{3}$,0),B(0,-30),一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为$\frac{9\sqrt{3}}{π}$ 秒.
如图,在平面直角坐标系中,直线AB交x、y轴于点A(10$\sqrt{3}$,0),B(0,-30),一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为$\frac{9\sqrt{3}}{π}$ 秒.
分析 根据题意画出图形,得出第一次与AB相切时,O正好在∠OAC的角平分线上,求出∠OAB的度数,求出∠OAM,根据三角函数值求出AM、求出OM,根据动圆每6秒滚动一圈即可求出动圆与直线AB第一次相切时所用的时间.
解答  解:如图当⊙O于AB第一次相切时,于x轴切于M,此时O正好在∠OAC的角平分线上,
解:如图当⊙O于AB第一次相切时,于x轴切于M,此时O正好在∠OAC的角平分线上,
∵A(10$\sqrt{3}$,0),B(0,-30),
∴OA=10$\sqrt{3}$,OB=30,
∴tan∠OAB=$\frac{30}{10\sqrt{3}}$=$\sqrt{3}$,∴∠OAB=60°,∴∠OAM=60°,
∵OM=3,∴tan60°=$\frac{OM}{AM}$=$\frac{3}{AM}$,∴AM=$\sqrt{3}$,
∴OM=10$\sqrt{3}-\sqrt{3}=9\sqrt{3}$,
设动圆与直线AB第一次相切时所用的时间是x秒,
∵动圆每6秒滚动一圈,
∴$\frac{2π×3}{6}$=$\frac{9\sqrt{3}}{x}$,
解得:x=$\frac{9\sqrt{3}}{π}$.
故答案为:$\frac{9\sqrt{3}}{π}$.
点评 本题考查了切线的性质,特殊角的三角函数值,圆的性质等知识点,关键是能根据题意画出图形,并知道主要应该求那一条线段的长,题目比较难懂,是有一定难度的题目.

练习册系列答案
相关题目
5.设集合A={x||x-2|≤2,x∈R},B={y|y=-x2,-1≤x≤2},则A∩B等于( )
| A. | R | B. | {0} | C. | {x|x∈R,x≠0} | D. | ∅ |
9.已知线段PQ两端点的坐标分别为(-1,1),(2,2),若直线l:x+my+m=0与线段PQ有交点,则m的范围是( )
| A. | $(-∞,-\frac{2}{3}]∪[\frac{1}{2},+∞)$ | B. | $[-\frac{2}{3},\frac{1}{2}]$ | C. | $(-∞,-\frac{3}{2}]∪[2,+∞)$ | D. | $[-\frac{3}{2},2]$ |
19.已知 f(x)=$\left\{\begin{array}{l}{x-1,x>0}\\{π,x=0}\\{x+2,x<0}\end{array}\right.$ 则f{f[f(-1)]}=( )
| A. | -2 | B. | 1 | C. | π | D. | 2 |
6.若复数z=$\frac{i}{-1+2i}$,则$\overline{z}$的虚部为( )
| A. | -$\frac{1}{5}$i | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$i | D. | $\frac{1}{5}$ |
3.直线2x+y+3=0在y轴上的截距是( )
| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | 3 | D. | -3 |
 一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2016分钟结束之时,质点的位置坐标是(44,8).
一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2016分钟结束之时,质点的位置坐标是(44,8).